1.2.2. Определение валентных состояний атомов в рамках остовно-электронной концепции строения минералов и других твердых тел

В современной кристаллохимической литературе вопрос о валентности[1], т. е. числе участвующих в связях электронов у атомов, образующих химические соединения, освещен явно недостаточно, а точнее односторонне. Дело в том, что в гетероатомных неорганических кристаллах (к которым относится большинство минералов) обычно ясна валентность катионных, но не анионных компонентов. Такая ситуация традиционно объясняется тем, что до сих пор во всех современных учебниках и справочниках по химии распространены предельно-ионные модели кристаллов типа Na⁺Cl^-, Cu⁺Cl^-, Mg²⁺O^2-, Ве²⁺O^2-, Zn²⁺S^2-, Al³⁺N^3-, Al₂³⁺O₃^2-, Si⁴⁺O₂^2- и др., в которых (по соответствующим степеням окисления) галоид одновалентен, кислород и сера двухвалентны, а азот трехвалентен. Однако фактическая валентность неметаллов в соединении далеко не всегда совпадает с их степенями окисления, что в физике полупроводников было известно уже давно. Так, в соответствии с правилом Гримма-Зоммерфельда в кристаллах с тетраэдрической координацией атомов и двухэлектронными связями sp³-типа хлор в CuCl семивалентен, кислород в ВеО и сера в ZnS шестивалентны, азот в AlN пятивалентен и т. д. Здесь уместно упомянуть о дискуссии между такими крупнейшими учеными, как Полинг и Филипс, по вопросу о фактическом числе участвующих в связях электронов у атомов в кристаллах (таблица 1.14). Таблица 1.14 Две трактовки электронного строения кристаллов с тетраэдрической координацией атомов согласно данным работы (Pauling, 1969; Phillips, 1969)

Кристаллы	Числа связующих электронов у атомов согласно
	Полингу	Филлипсу
СС	4+4 = 8e-	4+4 = 8e-
BN	3+3 = 6e-	3+5 = 8e-
BeO	2+2 = 4e-	2+6 = 8e-

Из этой таблицы следует, что Полинг, будучи апологетом классической теории валентности, постулирует неизменность, сохранение валентности обоих компонентов соединений при переходе от молекул к кристаллам (трехвалентость азота, двухвалентность кислорода). Филипс же, оперируя соответствующими спектроскопическими данными, доказывает пятивалентность азота в кристалле BN и шестивалентность кислорода в кристалле ВеО. Таким образом, даже у крупнейших ученых нет единого мнения по обсуждаемой проблеме. Естественно, возникает вопрос: какова же фактическая валентность неметаллов в таких, например, кристаллах, как NaCl, MgO, ВеО, Al₂O₃, SiO₂? В большинстве современных учебников по структурной химии, кристаллохимии и минералогии (Бокий, 1971; Урусов, 1975; Уэллс, 1987, 1988; Marfunin, 1994), к сожалению, нет ответа на этот вопрос. Имеющиеся же в литературе соответствующие данные скудны и противоречивы. Так, одна из альтернатив (выше упомянутая в связи с дискуссией Полинг-Филлипс) решения данного вопроса утверждает сохранение валентностей атомов при переходе от молекулы к кристаллу. Например, С. С. Бацанов, ссылаясь на Л. Полинга, пишет (Бацанов, 2000, с. 275): «в кристалле, например, NaCl может существовать только одна нормальная химическая связь Na-Cl, а с остальными лигандами атом натрия может взаимодействовать только электростатическим способом». Понятно, что эта ситуация соответствует одновалентному состоянию хлора в кристалле и остовно-электронной формуле [Na⁺](0,33e^-)₆[Cl⁺]. Итак, согласно этому подходу, на формульную единицу кристалла NaCl приходится одна (0,33e^-x6 = 2e^-) делокализованная двухэлектронная связь Na-Cl. Другой подход, наиболее последовательно отстаиваемый Сандерсэном соответствующими энергетическими расчетами (Sanderson, 1983), предполагает, что на формульную единицу кристалла NaCl (как и многих других галоидов щелочных металлов) приходится 4 двухэлектронных делокализованных связи Na-Cl, что можно отразить в виде следующей остовно-электронной формулы [Na⁺](1,33e^-)₆[Cl⁷⁺] с семивалентным хлором. Таким образом, имеются явно противоречащие друг другу точки зрения по вопросу о валентности хлора в кристалле NaCl, и целесообразность обсуждения данного вопроса очевидна. Первая систематическая попытка его решения была предпринята в рамках остовно-электронной концепции строения минералов (Минералогический справочник, 1985; Зуев, 1990). Однако в указанных и других предыдущих работах (Сюше, 1969; Тимесков, 1969; Макаров, 1981; Семенов, 2001) выбор тех или иных валентных состояний (зарядов атомных остовов) неметаллов в кристаллах зачастую был сделан довольно формально (произвольно) без надлежащего энергетического обоснования. В частности, в моделях конституции минералов по Тимескову принимаются максимально возможные (групповые) валентные состояния неметаллов согласно их положению в той или иной группе Периодической системы. В работах Семенова оценка валентности (заряда остова) кислорода в простых и сложных кристаллических оксидах принимается из расчета, чтобы электронные заряды межатомных связей имели целочисленные (кратные заряду электрона) значения, что представляется довольно искусственным приемом. Цель данного раздела - внести соответствующие уточнения, касающиеся истинных валентностей атомов в минералах по сравнению с нашими предыдущими данными (Зуев, 1990). Как оказалось, озаглавленная проблема вполне успешно решается при использовании параметров энергии сцепления атомных остовов и связующих электронов в рассматриваемых кристаллических соединениях при оценке их твердости. Для этого достаточно обратиться к результатам расчетов по следующим формулам (Зуев, 2002; см. также формулы (1.17-1.19) в предыдущем разделе):

W = ΣI_n + E_α; W_v = (W/M)ρ; Н_М = 3,5W_v, (1.20)

в которых W - энергия сцепления атомных остовов и связующих электронов (МДж/моль); ΣI_n - сумма потенциалов ионизации атомов или энергия образования атомных остовов из свободных нейтральных атомов (МДж/моль)[2]; E_α - энергия атомизации (энергия сцепления атомов) соединения (МДж/моль); W_v - удельная объемная энергия сцепления атомных остовов и связующих электронов соединения (МДж/см³); M - его молекулярный вес (г/моль); ρ - плотность (г/см³); Н_М - относительная твердость по 15-балльной минералогической шкале. В качестве примеров рассмотрим ряд простых и сложных кристаллических соединений из различных классов: ковалентных, ионно-ковалентных, металлических и ионно-ковалентно-металлических. В кристалле алмаза - типичного ковалентного соединения четырехвалентный углерод в состоянии 2sp³-гибридизации образует двухэлектронные связи С-С. Поэтому единственным вариантом строения алмаза будет остовно-электронная модель (Зуев, 1990) - |[C⁴⁺](2e^-)₄[C⁴⁺]| По формулам (1.20) W = I₁ + I₂ + I₃ + I₄ + E_α = 1,086 + 2,352 + 4,62 + 6,222 + 0,714 = 14,99 МДж/моль[3], W_v = (14,99/12,01)x3,52 = 4,39 МДж/см3, Н_М = 3,5x4,39 = 15,4, что соответствует справочным данным (Поваренных, 1963). Второй пример - ионный, а, точнее, ковалентно-ионный кристалл виллиомита NaF, обладающий кубической координационной структурой (типа NaCl) с октаэдрической координацией атомов. В силу его диамагнетизма для кристалла NaF имеет смысл рассмотреть 4 варианта электронного строения с нечетной меняющейся валентностью фтора: 1, 3, 5 и 7. Из таблицы 1.15 следует однозначный выбор в пользу второго варианта с остовами [Na⁺] и [F³⁺], поскольку в том случае расчетная твердость кристалла NaF почти в точности равна экспериментальной. Аналогичный результат получается для флюорита в случае принятия для него модели с остовами [Ca²⁺] и [F³⁺] и одноэлектронными связями Ca-F (таблица 1.16). Для селлаита MgF₂ совпадение расчетной и экспериментальной твердости (4,5) получается в случае принятия остовов [Mg²⁺] и [F³⁺]. Расчетная твердость кристалла LiF (структура типа NaCl) в предположении остовного состава Таблица 1.15 Варианты остовно-электронного строения кристалла NaF (виллиомита) в сопоставлении с расчетной твердостью (справочная твердость 3)

Вариантыостовов	Заряд связи q(Na-F), e-	W,МДж/моль	Wv,МДж/см3	НМ
[Na+][F+]	0,33	2,94	0,20	0,7
[Na+][F3+]	0,67	12,36	0,82	2,9
[Na+][F5+]	1,0	31,79	2,12	7,4
[Na+][F7+]	1,33	65,27	4,35	≥15

Таблица 1.16 Варианты остовно-электронных моделей флюорита CaF₂ в сопоставлении с расчетной твердостью (справочная твердость 4)

Вариантыостовов	Заряд связиq(Ca-F), e-	W,МДж/моль	Wv,МДж/см3	НМ
[Ca2+][F+]2	0,5	6,67	0,27	1,0
[Ca2+][F3+]2	1,0	25,51	1,04	3,6
[Ca2+][F5+]2	1,5	64,37	2,62	9,2
[Ca2+][F7+]2	2,0	131,33	5,35	>15

[Li⁺][F³⁺]оказалась равной 4,4 в согласии со справочной твердостью (4,5) по данным (Акустические кристаллы, 1982). Для обладающего структурой типа кварца кристалла BeF₂ близость расчетной и экспериментальной твердости (4-4,5) имеет место в случае принятия в этом кристалле остовов [Be²⁺] и [F³⁺]. Для сложных кристаллических фторидов, например, криолитионита Na₃Al₂Li₃F₁₂ в предположении остовного состава [Na⁺]₃[Al³⁺]₂x[Li⁺]₃[F³⁺]₁₂ получаются следующие данные: W = 155,68 МДж/моль, W_v = 1,15 МДж/см³ и Н_М = 4 (экспериментальная твердость по разным источникам от 3 до 5). Таким образом, в кристаллических фторидах, по всей вероятности, реализуются остовы [F³⁺]. Следует подчеркнуть один важный момент. Неметаллы могут участвовать в соединениях как в виде полных атомных остовов с зарядами, соответствующими номеру группы Периодической системы, так и в виде атомных остовов с неподеленными электронами. Последнее относится, в первую очередь, к высокоэлектроотрицательным неметаллам (O, F и др.), остовы которых способны прочно удерживать свои внутренние потенциально валентные электроны. В рассмотренных фторидах эту ситуацию можно представить в виде полного заряда остова с двумя неподеленными парами электронов - [(F⁷⁺)4e^-] = [F³⁺]. По данным таблицы 1.17 для кристалла галита NaCl делается выбор в пользу остовно-электронной модели с остовами [Na⁺][Cl⁵⁺] и одноэлектронными связями Na-Cl. Аналогичным образом - по соответствию расчетной и экспериментальной твердости - доказывается, что в строении других кристаллических хлоридов принимают участие Таблица 1.17 Варианты остовно-электронных моделей галита NaCl в сопоставлении с расчетной твердостью (экспериментальная твердость 1,6-2,5)

Вариантыостовов	Заряд связиq(Na-Cl), e-	W,МДж/моль	Wv,МДж/см3	НМ
[Na+][Cl+]	0,33	2,39	0,09	0,3
[Na+][Cl3+]	0,67	8,51	0,31	1,1
[Na+][Cl5+]	1,0	20,21	0,75	2,6
[Na+][Cl7+]	1,33	40,59	1,5	5,2

именно остовы [Cl⁵⁺]. Так, если принять для гидрофилита CaCl₂ остовы [Ca²⁺] и [Cl⁵⁺], то расчеты дают W = 41,09 МДж/моль, W_v = 0,82 МДж/см³ и Н_М = 2,9 (экспериментальная твердость равна 3). Таким образом, в отличие от фторидов, в кристаллических хлоридах могут иметь место более высоко зарядные остовы хлора (например, с одной неподеленной парой электронов - [(Cl⁷⁺)2e^-] = [Cl⁵⁺]). Различие в зарядах остовов фтора и хлора в кристаллических соединениях естественным образом объясняется значительным различием электроотрицательностей атомов (F - 4, Cl - 3), благодаря чему более электроотрицательный остов [F⁷⁺] способен удерживать две неподеленные пары электронов, а менее элетроотрицательный остов [Cl⁷⁺] - одну неподеленную пару электронов. Следует оговориться, что тенденция реализации остовов [Cl⁵⁺] в кристаллических хлоридах справедлива, строго говоря, лишь для координационных соединений с высокими КЧ(Cl), поэтому ее не следует абсолютизировать. В частности, в кристалле AlCl₃, обладающим слоистой структурой с октаэдрической координацией алюминия и двойной уголковой хлора, реализуются, по всей вероятности, остовы [Cl³⁺]. Соответствующая остовно-электронная формула с двухэлектронными связями Al-Cl будет [Al³⁺](2e^-)₆[Cl³⁺]₃, для которой расчеты дают W = 28,66 МДж/моль, W_m = 0,215 МДж/г и максимальную частоту колебания атомов по ниже приведенной формуле (1.21) v_m = 7 ТГц в согласии со справочными данными (Мамыров, 1991). Далее рассмотрим координационные кристаллические оксиды различных валентных типов М₂О, МО и МО₂. По данным таблицы 1.18 обладающий структурой типа антифлюорита кристалл Na₂O построен из остовов [Na⁺] и [O⁴⁺], поскольку его экспериментальная относительная твердость близка к 2,5. Аналогичным образом для кристалла периклаза MgO (экспериментальная твердость которого около 6) из трех теоретически возможных принимается остовно-электронная модель с остовами [Mg²⁺] и [O⁴⁺] и одноэлектронными связями Mg-O (таблица 1.19)[4], а для кристалла кварца SiO₂ (экспериментальная твердость которого около 7) делается выбор в пользу остовно-электронной модели с остовами [Si⁴⁺] и [O⁴⁺] и трехэлектронными (полуторного порядка) связями Si-O (таблица 1.20). Таблица 1.18 Варианты остовно-электронных моделей кристалла Na₂O в сопоставлении с расчетной твердостью

Вариантыостовов	Заряд связиq(Na-O), e-	W,МДж/моль	Wv,МДж/см3	НМ
[Na+]2[O2+]	0,5	7,89	0,3	1,0
[Na+]2[O4+]	0,75	19,34	0,75	2,6
[Na+]2[O6+]	1,0	43,66	1,69	5,9

  Таблица 1.19 Варианты остовно-электронных моделей периклаза MgO в сопоставлении с расчетной твердостью

Вариантыостовов	Заряд связиq(Mg-O), e-	W,МДж/моль	Wv,МДж/см3	НМ
[Mg2+][O2+]	0,33	7,89	0,7	2,5
[Mg2+][O4+]	1,0	20,66	1,83	6,4
[Mg2+][O6+]	1,33	44,97	3,99	14

Таблица 1.20 Варианты остовно-электронных моделей кварца SiO₂ в сопоставлении с расчетной твердостью

Вариантыостовов	Заряд связиq(Si-O), e-	W,МДж/моль	Wv,МДж/см3	НМ
[Si4+][O2+]2	2,0	21,23	0,94	3,3
[Si4+][O4+]2	3,0	46,77	2,06	7,2
[Si4+][O6+]2	4,0	95,4	4,21	14,7

  Особого внимания заслуживают данные таблицы 1.20 для кварца, в которой фактически решается принципиальный вопрос о порядке (кратности) кремнекислородных связей в этом минерале. Дело в том, что до сих пор авторы некоторых квантово-химических расчетов продолжают настаивать на ординарных связях Si-O в модификациях SiO₂ с тетраэдрической координацией атомов кремния (включая кварц). Однако из таблицы 1.20 следует невозможность как ординарных, так и двойных кремнекислородных связей в кварце, тогда как полуторный порядок этих связей наиболее вероятен, поскольку находится в соответствии с твердостью минерала, обусловленной соответствующей энергией сцепления атомных остовов и связующих электронов. До сих пор мы рассматривали простые (бинарные) кристаллические соединения. Разумеется, аналогичный подход возможен и по отношению к более сложным кристаллам. В качестве первого примера обратимся к форстериту Mg₂SiO₄. В некоторых предыдущих работах (Тимесков, 1969; Макаров, 1979; Зуев, 1990) принимается общее число валентных электронов в форстерите равным 32e^-, что соответствует проявлению максимально возможной валентности кислорода или, другими словами, остовам [O⁶⁺]. Однако по параметрам W_v и Н_М (таблица 1.21) в форстерите, экспериментальная (справочная) твердость которого близка к 7 (Зуев, 1990), кислород реализуется в виде остовов [O⁴⁺], как и в кристаллах MgO и SiO₂. Наличие неподеленных электронов у шестизарядного остова кислорода в форстерите следует из прецизионных расчетов деформационной электронной плотности (Van der Wal, Vos, 1987). Таблица 1.21 Варианты остовного состава форстерита a-Mg₂SiO₄ в сопоставлении с расчетной твердостью

Варианты остовов	W, МДж/моль	Wv, МДж/см3	НМ
[Mg2+]2[Si4+][O2+]4	34,14	0,77	2,7
[Mg2+]2[Si4+][O4+]4	88,15	2,00	7
[Mg2+]2[Si4+][O6+]4	185,41	4,22	14,8

Аналогичные данные о кислородных остовах [O⁴⁺] были получены для многих других простых и сложных координационных (а также каркасных) кристаллических соединений (BeO, Al₂O₃, Fe₂O₃, CaO, BaO, ZnO, CuO, CuFeO₂, MgAl₂O₄, BeAl₂O₄, FeFe₂O₄, CaTiO₃, FeTiO₃, Be₂SiO₄, FeWO₄, Ca₃Al₂Si₃O₁₂ и др.). Таким образом, вывод о весьма распространенном (универсальном) четырехвалентном состоянии кислорода в оксидных кристаллах можно считать энергетически доказанным, что представляется весьма важным для неорганической кристаллохимии вообще.[5] Это состояние остова кислорода [O⁴⁺] = [(O⁶⁺)2e^-] со сферической внешней неподеленной парой 2s²-электронов идеально подходит для построения координационных кристаллов, поскольку предполагает возможность реализации практически любых КЧ кислорода. Кроме того, имеет смысл еще раз подчеркнуть, что повышенная стабильность и соответственно распространенность четырехвалентного состояния кислорода, его способность прочно удерживать остовом [O⁶⁺] неподеленную пару электронов в кристаллических оксидах объясняются высокой электроотрица-тельностью кислорода. Корректность принятия остовов [O⁴⁺] в силикатах доказывается, в частности, критерием межатомных расстояний, что следует из следующих данных:

минерал	формула	q(Si-O), e-	d(Si-O), Å
кварц	SiO2	3,0	1,61
циркон	ZrSiO4	2,78	1,62
кианит	Al2SiO5	2,60	1,62
фенакит	Be2SiO4	2,36	1,63
форстерит	Mg2SiO4	2,36	1,64
гроссуляр	Ca3Al2Si3O12	2,26	1,65

Как видим, наблюдается четкая обратная зависимость длин связей Si-O от их электронных зарядов, рассчитанных (в случае принятия во всех этих минералах остовов [O⁴⁺]) по методикам автора (Зуев, 1990). С другими вариантами остовов кислорода - [O⁶⁺] в форстерите и гроссуляре, [O⁵⁺] в фенаките, принятыми нами ранее (Зуев, 1990), расчеты приводят к резкому нарушению выявленной естественной корреляции. Расчеты по формулам Кордеса (Kordes, 1964) и Приходько (Приходько, 1973) дают для радиуса остова [O⁶⁺] величину 0,11 Å, а для остова [O⁴⁺] величину 0,21 Å. Тот факт, что решетки кристаллов типа МО в большинстве случаев кристаллизуются в структурном типе галита-галенита с октаэдрической координацией атомов (КЧ = 6) находит следующее чисто геометрическое объяснение, исходящее из соотношения радиусов остова [O⁴⁺] и связующего электрида. В кристаллических оксидах типа MgO имеют место связывающие электриды с зарядом 1e^- (таблица 1.19), радиусы R которых можно оценить из данных для молекулы Н₂⁺. Ее остовно-электронная формула |[H⁺](1e^-)[H⁺]|, а межатомное расстояние d(H-H) = 1,06 Å. Поскольку Н⁺ является практически «бестелесным» ионом, то радиус однозарядного электрида R = 1,06/2 = 0,53 Å. Так как r_i(O⁴⁺) = 0,21 Å, то имеем отношение радиусов остова и электрида равным 0,21/0,53 = 0,4, которое идеально удовлетворяет именно октаэдрической координации кислорода (Гиллеспи, 1975). Заметим, что в случае принятия предельно-ионной модели, например, кристалла MgO, отношение ионных радиусов r_i(Mg²⁺) = 0,86 Å и r_i(O2-) = 1,26 Å (Современная кристаллография, 1979) составляет величину 0,86/1,26 = 0,68, которая, хотя и не противоречит октаэдрической координации атомов, но менее удовлетворительна по сравнению с предыдущей. Таким образом, в соответствии с остовно-электронным подходом октаэдрическая координация атомов в кристаллических оксидах типа МО в первую очередь определяется (диктуется) анионами кислорода, а точнее соответствующим соотношением размеров его остовов и связующих электридов. Твердость сложных кристаллических соединений с комплексными радикалами (нитратов, сульфатов) определяется прочностью слабых связей нерадикальных катионов с кислородом, и разрушение таких кристалллов происходит именно по этим связям. При этом прочные связи внутри радикалов сохраняются. Очевидно, что оценка твердости таких кристаллов по параметрам W_v не правомерна, поскольку этот параметр учитывает в усредненном виде энергию всех связей М-О (как нерадикальных, так и радикальных катионов). Поэтому в таблицу 1.22 продемонстрирован другой метод контроля остовного состава соединений - по соответствию расчетных и экспериментальных максимальных частот колебаний атомов (n_m, ТГц), вычисляемых по формуле (Зуев, 2002):

v_m = 19,3W_m^0,66, (1.21)

где W_m - удельная массовая энергия сцепления остовов и электронов соединения, вычисляемая по отношению W/M (см. формулу (1.17)). Таблица 1.22 Остовный состав, энергетические параметры и максимальные частоты колебания атомов в минералах с островным мотивом структуры (с радикалами NH₄⁺, NO₃^-, SO₄^2-, PO₄^3-, CO₃^2-, SiO₄^4-)

Минерал	Образующие кристаллическую решетку остовы	W,МДж/моль	Wm,МДж/г	nm, ТГц
				Расчет	(Мамыров,1991)
Фторид аммония	[N5+][H+]4[F3+]	42,57	1,15	21,16	20,47
Кальцинитрит	[Ca2+][N5+]2[O2+]6	85,01	0,518	12,51	12,36
Ангидрит	[Ca2+][S6+][O3+]4	71,31	0,52	12,55	12,32
Витлокит	[Ca2+]3[P5+]2[O4+]8	186,37	0,60	13,8	12,9
Кальцит	[Ca2+][C4+][O4+]3	71,28	0,71	15,4	14,5
Кальциоливин	[Ca2+]2[Si4+][O4+]4	87,44	0,51	12,39	13,35

Параметр W_m характеризует в некоторой усредненной форме колебания (и соответственно связи) всех атомов сложного (комплексного) кристаллического соединения безотносительно его структурного мотива. Для других кристаллических нитратов (KNO₃, NaNO₃, RbNO₃, CsNO₃, Sr(NO₃)₂, Ba(NO₃)₂) также получается близкое соответствие расчетных и экспериментальных величин n_m в случае принятия для атомов кислорода остовов [O2+]. Аналогичным образом - путем соответствующих расчетов - доказывается наличие остовов [O³⁺] в сульфатах (K₂SO₄, Na₂SO₄, MgSO₄, BaSO₄) и остовов [O⁴⁺] в фосфатах, карбонатах и силикатах. Во избежание недоразумений оговоримся, что принятие остова [O³⁺] в сульфатах не следует понимать буквально - как некоторое парамагнитное состояние кислорода. В силу очевидного факта диамагнетизма анионов O^2- в сульфатах запись [O³⁺] означает лишь то, что в этом случае заряд остова [O⁴⁺] экранирован зарядом половины двухэлектронного облака (неподеленной электронной пары), другая половина которого делокализована на связь с катионным компонентом сульфата: [O⁴⁺(2e^-)_1/2] = [O³⁺]. Именно в этом и только в этом смысле остов кислорода в сульфате может рассматриваться как промежуточный между остовами [O²⁺] и [O⁴⁺]. Аналогичная ситуация описана на примере остова [O⁵⁺] = [O⁶⁺(2e^-)_1/2] в некоторых минералах (Зуев, 1990, с. 86). Далее попытаемся распространить продемонстрированный на примере оксидов подход к оценке валентного состояния серы в сульфидах. Подходящими для этой цели объектами являются сульфиды в изоструктурных парах кристаллов: Na₂O-Na₂S, MgO-MgS, CaO-CaS, SrO-SrS, BaO-BaS, BeO-BeS, ZnO-ZnS и т. д. Как было показано, кислород в указанных оксидах четырехвалентен. Расчеты валентности серы в сульфидах, по типу выполненных для оксидов, привели к неожиданному результату, а именно к шестивалентному состоянию серы, соответствующему остовам [S⁶⁺] (таблицы 1.23-1.25). Полученный результат можно объяснить тем, что по сравнению с кислородом сера является менее электроотрицательным неметаллом и поэтому способна отдавать для связей с катионными компонентами сульфидов все шесть внешних валентных электронов. Впрочем, в данном случае речь идет не о строгой закономерности, а, скорее всего, о некоторой тенденции, которую можно сформулировать так: в координационных бинарных кристаллах оксидов кислород чаще всего реализуется в виде остовов [O⁴⁺], а в соответствующих сульфидах - в виде остовов [S⁶⁺].[6] Сходная ситуация, как было показано выше, имеет место при сопоставлении координационных кристаллических фторидов (с остовами [F³⁺]) и хлоридов (с остовами [Cl⁵⁺]). Таблица 1.23 Варианты остовно-электронных моделей кристаллов Na₂S и MgS в сопоставлении с расчетной твердостью (экспериментальная твердость первого 2,5, второго около 5)

Варианты остовов	Заряд связиq(M-S), e-	W,МДж/моль	Wv,МДж/см3	НМ
[Na+]2[S2+]	0,5	5,09	0,12	0,4
[Na+]2[S4+]	0,75	13,02	0,31	1,1
[Na+]2[S6+]	1,0	28,53	0,68	2,4
[Mg2+][S2+]	0,67	6,31	0,29	1,0
[Mg2+][S4+]	1,0	14,23	0,67	2,3
[Mg2+][S6+]	1,33	29,74	1,40	4,9

Таблица 1.24 Варианты остовно-электронных моделей сфалерита ZnS в сопоставлении с расчетной твердостью (экспериментальная твердость близка к 4)

Варианты остовов	Заряд связиq(Zn-S), e-	W,МДж/моль	Wv,МДж/см3	НМ
[Zn2+][S2+]	1,0	6,5	0,27	0,95
[Zn2+][S4+]	1,5	14,42	0,61	2,1
[Zn2+][S6+]	2,0	29,93	1,26	4,4

Таблица 1.25 Варианты остовно-электронных моделей кристалла BeS (тип вюртцита) в сопоставлении с расчетной твердостью (экспериментальная твердость 6)

Варианты остовов	Заряд связи q(Be-S), e-	W,МДж/моль	Wv,МДж/см3	НМ
[Be2+][S2+]	1,0	6,75	0,39	1,4
[Be2+][S4+]	1,5	14,67	0,84	2,9
[Be2+][S6+]	2,0	30,18	1,73	6,0

Следует заметить, что принимаемый в работе (Семенов, 2000) вариант сфалерита с остовами [Zn²⁺][S²⁺] и одноэлектронными связями Zn-S абсолютно не приемлем с точки зрения твердости (таблица 1.24), тогда как традиционная трактовка сфалерита как полупроводника валентного типа АIIBVI с двухэлектронными связями находится в полном соответствии с микротвердостью сфалерита (Лебедева, 1963). Для близкого по структуре кристалла цинкита ZnO (тип вюртцита) расчет твердости в случае принятия остовов [Zn²⁺][O⁶⁺] дает заведомо завышенную величину Н_М = 11, а для варианта с остовами [Zn²⁺][O⁴⁺] расчетная твердость цинкита отвечает справочной (Н_М = 5). Аналогичным образом для изоструктурного кристалла бромеллита ВеО расчет твердости в случае принятия остовов [Be²⁺][O⁶⁺] приводит к неприемлемой величине Н_М = 19 (твердость выше алмаза!), а для варианта с остовами [Be²⁺][O⁴⁺] расчетная твердость отвечает приводимой в большинстве минералогических справочников (Н_М = 9). Для изоструктурного со сфалеритом сложного сульфида станнина Cu₂FeSnS₄ (в предположении, что решетка минерала образована остовами [Cu⁺]₂[Fe²⁺][Sn⁴⁺][S⁶⁺]₄) расчеты дают W = 122,0 МДж/моль, W_v = 1,25 МДж/см³ и Н_М = 4,3 в полном согласии с экспериментальной твердостью этого минерала (Лебедева, 1963). Специально остановимся на определении валентности атомов в кристаллах металлов, что представляется особенно важным для переходных элементов с переменной валентностью. Сначала рассмотрим триаду металлов Cu-Ag-Au, обладающих ГЦК-решеткой с КЧ = 12. В силу диамагнетизма (отсутствия неспаренных электронов) в металлической меди имеет смысл рассмотреть три варианта остовно-электронных моделей соответственно с остовами [Cu⁺], [Cu³⁺] и [Cu⁵⁺]. Как показали расчеты, лишь второй вариант с трехвалентной медью удовлетворяет справочной твердости этого металла, а для электронных аналогов меди - серебра и золота - близкие к справочным твердости обоих металлов получаются в случае принятия в них дробных валентностей[7], весьма близких, однако, также к трехвалентному состоянию (таблица 1.26). Другой пример - железо модификации α-Fe с ОЦК-решеткой (КЧ = 8). До настоящего времени вопрос о валентности атомов в металлическом железе остается открытым и дискуссионным. Допускаются различные варианты числа вовлекаемых в химическую связь электронов у атомов железа: 2 (Григорович, 1988), 3 (Поваренных, 1963), 4 (Зуев, 1997), 4,71 (Регель и Глазов, 1978), 5,78 и 6 (Pauling, 1960). По данным таблицы 1.27 экспериментальной твердости железа (4-5 по разным источникам) ближе всего вариант с зарядом атомного остова, промежуточным между остовами [Fe³⁺] и [Fe⁴⁺]. Этот вариант соответствует валентности поверхностных атомов металлического железа по данным работы (Яковлев, 1994). Таблица 1.26 Остовно-электронные модели, энергетические параметры и расчетные твердости меди, серебра и золота

Остовы металлов	Заряд связиq(M-M), e-	W,МДж/моль	Wv,МДж/см3	НМ
[Cu3+]	0,50	6,60	0,89	3,1
[Ag3.2+]	0,53	7,45	0,72	2,5
[Au3.3+]	0,55	7,37	0,72	2,5

Таблица 1.27 Варианты остовно-электронных моделей металлического железа (модификации α-Fe) в сопоставлении с расчетной твердостью

Варианты остовов	Заряд связиq(Fe-Fe), e-	W,МДж/моль	Wv,МДж/см3	НМ
[Fe2+]	0,5	2,74	0,39	1,3
[Fe3+]	0,75	5,69	0,80	2,8
[Fe4+]	1,0	10,98	1,55	5,4
[Fe6+]	1,5	27,82	3,92	13,7

Аналогичными расчетами доказывается четырехвалентность металла в платине (ГЦК-решетка с КЧ = 12, остовы [Pt⁴⁺], заряды связей q(Pt-Pt) = 0,67e-, W = 9,92 МДж/моль, W_v = 1,1 МДж/см³, расчетная твердость Н_М = 3,85 близка к справочной Н_М = 4). Используя продемонстрированную методику, можно уточнять (исправлять) имеющиеся данные по валентности атомов в некоторых металлах. В частности, по нашим оценкам, таллий и индий в металлах получаются трехвалентными вопреки данным об одновалентном состоянии атомов в этих металлах согласно оценкам А. С. Поваренных (Поваренных, 1963). Наиболее сложными объектами для оценки валентных состояний атомов являются сульфиды (и их аналоги) переходных металлов, в которых наряду с ионно-ковалентными связями M-S присутствуют связи М-М (металлическое взаимодействие) (Зуев, 1990), благодаря чему фактическая валентность переходного металла в таких соединениях является неопределенной, а точнее сказать, до сих пор точно не установленной. Речь идет о таких весьма распространенных минералах, как пирит, пирротин, галенит, халькозин и многих других. Присутствие металлического межатомного взаимодействия определяет многие специфические свойства таких минералов: характерный металлический блеск, непрозрачность в видимой области спектра, высокую отражательную способность и т. д. Примесь металлической связи в указанных и других сульфидах доказывается критерием твердости (Зуев, 1990) и расчетами электронной плотности. Очевидно, что в рассматриваемых соединениях общий заряд атомного остова металла является суммой двух составляющих, соответствующих ионно-ковалентному и металлическому взаимодействию. Например, в галените PbS свинец по отношению к сере является двухвалентным. Но, находясь в IV группе Периодической системы, Pb потенциально четырехвалентен, т. е. для связей Pb-Pb можно предположить участие остальных двух (4-2) электронов. Тогда для межатомных связей в PbS используются все 6s²p² валентных электронов Pb, и его общий заряд остова будет [Pb⁴⁺]. По данным (Сюше, 1969; Зуев, 1990) атомы серы в галените используют для связей 3p⁴-электроны, причем электронная пара 3s² остается инертной (неподеленной). Следовательно, решетку галенита можно считать построенной из остовов [Pb⁴⁺] и [S⁴⁺]. Для соответствующей остовно-электронной модели расчеты приводят к W = 21,07 МДж/моль, W_v = 0,67 МДж/см³ и Н_М = 2,4 (экспериментальная твердость галенита составляет порядка 2,5). Естественно возникает вопрос, какие части (доли) энергии остовно-электронного взаимодействия (21,07 МДж/моль) приходятся на связи Pb-S и связи Pb-Pb? Соответствующую оценку можно сделать, абстрагируясь от примеси металлического взаимодействия Pb-Pb и рассмотрев остовно-электронную модель из остовов [Pb²⁺] и [S⁴⁺], для которой расчет дает W = 13,96 МДж/моль. Тогда на долю энергии металлического взаимодействия Pb-Pb в галените приходится 21,07-13,96 = 7,11 МДж/моль или (7,11/21,07)x100% = 34%, а на доминирующую часть энергии ионно-ковалентного взаимодействия Pb-S приходится 66%. Соответственно твердость галенита можно разложить на ионно-ковалентную составляющую твердости Н_Мi+c = 2,5x0,66 = 1,65 и металлическую составлющую Н_М^m= 2,5x0,34 = 0,85, сумма которых или общая (total) твердость галенита Н_М^t = 1,65+0,85 = 2,5. Исходя из зарядов атомных остовов и структурных данных (КЧ(Pb) = 6(S) + 12(Pb)), возможна раздельная оценка электронных зарядов связей: q(Pb-S) = 2/6+4/6 = 1,0e^- и q(Pb-Pb) = 2/12+2/12 = 0,33e^-. Следует также оговориться, что металлическое взаимодействие в силу гомоатомной природы не влияет на степень окисления (валентность) металла по отношению к неметаллу. Поэтому при оценке полярного характера связей M-S (и далее эффективных зарядов атомов) примесью металлических связей можно пренебречь (Зуев, 1990) и рассматривать, например, решетку галенита, образованную остовами [Pb2+] и [S4+]. При этом электроны металлической связи делятся пополам и соответствующим образом экранируют полный заряд атомного остова: [(Pb4+)2e-] = [Pb²⁺]. Итак, продемонстрированные на примере галенита расчеты дают уникальную возможность разложения общей энергии межатомного взаимодействия соединения на ионно-ковалентный и металлический вклады и, тем самым, впервые количественно оценивать долю примеси металлической связи в сульфидах и их аналогах. Соответствующие данные для обширной группы подобных соединений приведены в таблице 1.28, в которой для катионных компонентов общий заряд атомного остова (помещенный в круглых скобках) представлен в виде суммы двух слагаемых. Первое слагаемое отвечает валентности металла по отношению к неметаллу, а второе слагаемое - металлической валентности, т. е. первое слагаемое определяет количество электронов металла, участвующих в связях M-X, а второе - в связях М-М. Следует обратить внимание на одну любопытную закономерность. Расчеты показали, что в сульфидах (и их аналогах) с одновалентной медью фактически реализуются остовы [Cu⁽¹⁺²⁾⁺] = [Cu³⁺], которые, как было показано, имеют место в металлической меди. В сульфидах с двухвалентным железом (пирите, троилите и др.) общий заряд его атомного остова [Fe⁴⁺] близок к заряду атомного остова в кристалле металлического железа (α-Fe) (таблица 1.27). Таблица 1.28 Остовно-электронный состав минералов с примесью металлических связей с данными энергетических параметров сцепления остовов и валентных электронов, расчетной и экспериментальной твердости и доли металлической связи

Названиеминерала	Формула из образующих кристаллическую решетку остовов	Σe-	W,МДж/моль	Wv,МДж/см3	НМ (р)/НМ (э)	fm
Галенит	[Pb(2+2)+][S4+]	8	21,07	0,67	2,4/2,5	0,33
Клаусталит	[Pb(2+2)+][Se4+]	8	19,94	0,58	2,0/2,3	0,36
Алтаит	[Pb(2+2)+][Te4+]	8	18,76	0,465	1,6/2,3	0,38
Кристалл GeS	[Ge(2+2)+][S4+]	8	21,91	0,84	2,9/3,0	0,34
Троилит	[Fe(2+2)+][S4+]	8	22,54	1,24	4,3/4,25	0,37
Миллерит	[Ni(2+2)+[S4+]	8	23,15	1,35	4,7/5,0	0,38
Никеллин	[Ni(3+2)+][As3+]	8	24,6	1,44	5,0/5,5	0,52
Куперит	[Pt(2+4)+][S4+]	10	33,96	1,53	5,4/5,0	0,56
Брэггит	[Pd(2+2)+][S4+]	8	22,46	1,44	5,0/5,0	0,35
Котульскит	[Pd(2+2)+][Te6+]	10	32,65	1,3	4,5/4,5	0,23
Халькозин	[Cu(1+2)+]2[S4+]	10	24,73	0,9	3,1/2,8	0,45
Дигенит	[Cu(1+2)+]1.8[S4+]	9,4	23,40	0,91	3,2/3,0	0,42
Берцелианит	[Cu(1+2)+]1.96[Se4+]	9,9	23,31	0,8	2,8/3,0	0,48
Вейссит	[Cu(1+2)+]2[Te6+]	12	35,60	0,84	2,9/3,0	0,32
Акантит	[Ag(1+2)+]2[S4+]	10	24,39	0,72	2,5/2,5	0,46
Науманнит	[Ag(1+2)+]2[Se4+]	10	23,26	0,62	2,2/2,25	0,47
Гессит	[Ag(1+2)+]2[Te4+]	10	22,10	0,54	1,9/2,1	0,51
Умангит	[Cu(1.33+1.67)+]3[Se4+]2	17	38,29	0,75	2,6/3,0	0,39
Ялпаит	[Ag(1+2)+]3[Cu(1+2)+][S4+]2	20	49,35	0,74	2,6/2,5	0,46
Мальдонит	[Au(1.5+1.5)+]2[Bi(3+2)+]	11	27,30	0,71	2,5/2,5	0,67
Домейкит	[Cu(1+2)+]3[As5+]	14	36,55	1,03	3,6/3,5	0,78
Дискразит	[Ag(1+3)+]3[Sb5+]	17	50,27	1,08	3,8/3,75	0,85
Скуттерудит	[Co(3+2)+][As5+]3	20	68,32	1,64	6,0/6,0	0,16
Антимонит	[Sb(3+2)+]2[S4+]2[S2+]	20	56,56	0,79	2,8/3,0	0,34
Висмутин	[Bi(3+2)+]2[S4+]2[S2+]	20	56,08	0,75	2,6/3,0	0,34
Хизлевудит	[Ni(1.33+2.67)+]3[S4+]2	20	57,93	1,42	5,0/4,0	0,57
Стефанит	[Ag(1+2)+]5[Sb(3+2)+][S4+]4	36	93,24	0,74	2,6/3,0	0,40
Пирит	[Fe(2+2)+][S5+]2	14	48,06	2,01	7,0/7,0	0,19
Лаурит	[Ru(2+4)+][S5+]2	16	61,29	2,34	8,2/8,5	0,34
Эрликманит	[Os(2+4)+][S5+]2	16	58,28	2,19	7,7/7,5	0,30
Сперрилит	[Pt(4+4)+][As4+]2	16	63,28	1,91	6,7/6,5	0,67
Раммельсбергит	[Ni(4+2)+][As4+]2	14	50,6	1,73	6,0/5,9	0,34
Леллингит	[Fe(4+2)+][As4+]2	14	49,8	1,79	6,2/6,1	0,34
Калаверит	[Au(4+3)+][Te4+]2	15	50,58	1,04	3,6/4,0	0,43
Молибденит	[Mo(4+2)+][S4+]2	14	47,63	1,49	¾	0,30
Арсенопирит	[Fe(3+2)+][As4+][S5+]	14	47,40	1,80	6,3/6,5	0,25
Кобальтин	[Co(3+2)+][As4+][S5+]	14	47,84	1,79	6,3/6,5	0,29
Гудмундит	[Fe(3+2)+][As4+][S5+]	14	47,32	1,56	5,5/6,0	0,27
Халькопирит	[Cu(1+2)+][Fe(3+2)+][S4+]2	16	47,90	1,12	3,9/4,0	0,38
Борнит	[Cu(1+2)+]5[Fe(3+2)+][S4+]4	36	84,85	0,86	3,0/3,0	0,34
Энаргит	[Cu(1+2)+]3[As5+][S4+]4	30	82,49	0,93	3,3/3,0	0,20
Сульванит	[Cu(1+2)+]3[V5+][S4+]4	30	82,85	0,90	3,1/3,5	0,21
Прустит	[Ag(1+2)+]3[As3+][S4+]3	24	59,63	0,67	2,4/2,5	0,29
Пираргирит	[Ag(1+2)+]3[Sb3+][S4+]3	24	59,16	0,64	2,2/2,25	0,28
Буланжирит	[Pb(2+2)+]5[Sb(3+2)+]4[S4+]11	44	234,49	0,78	2,7/2,75	0,31
Гетероморфит	[Pb(2+2)+]7[Sb(3+2)+]8[S4+]19	144	414,24	0,78	2,7/2,75	0,32
Аргиродит	[Ag(1+2)+]8[Ge4+][S4+]6	52	182,77	0,73	2,5/2,5	0,34
Айкинит	[Cu(1+2)+][Pb(2+2)+][Bi(3+2)+][S4+]3	24	65,4	0,72	2,8/3,0	0,34
Бурнонит	[Cu(1+2)+][Pb(2+2)+][Sb(3+2)+][S4+]3	24	64,06	0,77	2,7/3,0	0,33
Зелигманит	[Cu(1+2)+][Pb(2+2)+][As(3+2)+][S4+]3	24	67,39	0,84	2,9/3,0	0,31
Тетраэдрит	[Cu(1+2)+]10[Cu(2+1)+]2[Sb(3+2)+]4[S4+]13	108	288,89	0,87	3,0/3,0	0,35
Бетехтинит	[Cu(1+2)+]16[Cu(2+1)+]5[Pb(2+2)+]2[S4+]15	131	332,83	0,92	3,2/3,0	0,38
Диафорит	[Ag(1+2)+]3[Pb(2+2)+]2[Sb(3+2)+]3[S4+]8	68	178,88	0,79	2,8/2,75	0,35
Джемсонит	[Pb(2+2)+]4[Fe(2+2)+][Sb(3+2)+]6[S4+]14	106	300,4	0,82	2,9/3,0	0,32
Цилиндрит	[Pb(2+2)+]3[Sb(3+2)+]2[Sn4+]4[S4+]14	94	263,88	0,8	2,8/2,75	0,17
Козалит	[Pb(2+2)+]2[Bi(3+2)+]2[S4+]5	38	101,21	0,74	2,6/2,5	0,31
Лилианит	[Pb(2+2)+]3[Bi(3+2)+]2[S4+]6	46	130,06	0,75	2,6/2,5	0,33
Галеновисмутит	[Pb(2+2)+][Bi(3+2)+]2[S4+]4	30	85,1	0,81	2,8/3,0	0,31
Виттихенит	[Cu(1+2)+]3[Bi(3+2)+][S4+]3	26	69,40	0,91	3,2/3,0	0,39
Со-пентландит	[Co(2+2)+]9[S4+]8	68	191,62	1,25	4,4/4,5	0,39
Петцит	[Ag(1+2)+]3[Au(1+2)+][Te4+]2	20	44,22	0,52	1,8/2,0	0,5
Ковеллин	[Cu(1+2)+]2[Cu(2+1)+][S3+]2[S4+]	19	43,84	0,71	2,5/2,5	0,33
Полибазит	[Ag(1+2)+]16[Sb(3+2)+]2[S4+]11	102	260,12	0,71	2,5/2,5	0,41
Плагионит	[Pb(2+2)+]5[Sb(3+2)+]8[S4+]17	128	371,36	0,81	2,8/2,5	0,32
Ливингстонит	[Hg(2+2)+][Sb(3+2)+]4[S4+]7	52	154,70	0,86	3,0/3,0	0,31
Когенит	[Fe(2+2)+]3[C4+]	16	47,93	2,06	7,2/7,5	0,52
Кристалл WC	[W(4+2)+][C4+]	10	34,56	2,78	9,7/10	0,30
Кристалл W2C	[W(2+4)+]2[C4+]	16	54,08	2,40	8,4/9,0	0,63
Кристалл VC	[V(4+1)+][C4+]	9	31,31	2,7	9,5/9,0	0,21
Кристалл NbС	[Nb(4+1)+][C4+]	9	28,82	2,20	7,7/9,0	0,17
Кристалл TaC	[Ta(4+1)+][C4+]	9	27,78	2,07	7,2/7,5	0,15
Шрайберзит	[Fe(2+2)+]3[P5+]	17	50,49	1,76	6,2/7,0	0,50
Осборнит	[Ti(3+1)+][N5+]	9	35,81	3,15	11/10	0,12

åe^-  - сумма валентных электронов; Н_М (р)/Н_М (э) - Н_М расчет /Н_М эксперимент;

f_m      - доля металлической связи.

Итак, по данным таблицы 1.28 наличие металлических связей М-М во многих рудных минералах объективно доказывается критериями энергии сцепления атомных остовов и связующих электронов и относительной твердости. Для дополнительного подтверждения этого приведем соответствующие расчеты для обладающей одинаковой структурой пары минералов гауерит MnS₂ - пирит FeS₂. Судя по физическим свойствам (включая магнитные), а также кристаллохимическим данным (Pauling, 1960), в высокоспиновом гауерите MnS₂ заметное взаимодействие Mn-Mn отсутствует, а в низкоспиновом пирите FeS₂, как показано, металлические связи Fe-Fe имеют место. Тогда для гауерита, остовная формула которого, согласно (Зуев, 1990), [Mn²⁺][S⁵⁺]₂, расчеты приводят к W = 39,65 МДж/моль, W_v = 1,16 МДж/см³ и Н_М = 4,1 (справочная твердость гауерита по всем минералогическим источникам равна 4). Для пирита остовная формула, учитывающая примесь металлических связей, - [Fe⁽²⁺²⁾⁺][S⁵⁺]₂, W = 48,06 МДж/моль, W_v = 2,01 МДж/см³, Н_М = 7 (экспериментальная твердость пирита по разным источникам, включая данные микротвердости (Лебедева, 1963), составляет 6,5-7,6), а для варианта без учета металлических связей в пирите остовная формула [Fe²⁺][S⁵⁺]₂ и расчетная твердость Н_М = 5,7. Здесь уместно обратить внимание на работу (Jones, Nebitt, 2002), согласно которой в кристаллах FeS₂, FeAsS, FeAs₂ близость энергии связи остовных электронов железа интерпретируется как одинаковая валентность Fe²⁺, что представляется ошибочным. По нашему мнению, более корректно энергию связи остовных электронов атома (в данном случае Fe) связывать не с валентностью, а с эффективным зарядом атома (Зуев, 1990). Тогда, исходя из общепринятых валентностей железа в рассматриваемом ряду соединений (Fe²⁺S₂, Fe³⁺AsS, Fe⁴⁺As₂), расчеты приводят к близости в них эффективных зарядов атомов железа: Fe^+0.68S₂^-0.34, Fe^+0.72As^-0.27S^-0.45, Fe^+0.64As₂^-0.32 (Куликов, Зуев, Вайншенкер, 1978). Если же учесть металлическую валентность, то общее число валентных электронов железа в FeS₂ равно 4 (2+2), в FeAsS равно 5 (3+2) и в FeAs₂ равно 6 (4+2) (таблицы 1.28). Исключив металлическую компоненту валентности (2), получим в этом ряду соединений следующие валентности железа по отношению к неметаллам - Fe(II)S₂, Fe(III)AsS и Fe(IV)As₂, которые полностью соответствуют химической природе и свойствам этих кристаллических соединений. Для варианта леллингита с двухвалентным железом Fe(II)As₂ расчеты дают резко заниженные эффективные заряды Fe^+0.4As₂^-0.2 (Зуев, 1990), которые не приемлемы, поскольку выпадают из установленной нами закономерности близости эффективных зарядов Fe в ряду кристаллов FeS₂-FeAsS-FeAs₂. Следует обратить внимание на последний столбец таблицы 1.28, где впервые даны оценки доли металлической связи в сульфидах и их аналогах в виде параметра f_m, варьирующего в интервале от 0,12 до 0,85 и в среднем составляющего величину 0,36 (близкую к 0,33). Последняя величина доли металлической связи наиболее часто встречается для рассмотренных в таблице 1.28 минералов. Другими словами, в преобладающем числе этих минералов (сульфидов и их аналогов) межатомное взаимодействие приблизительно на 1/3 определяется металлическими связями М-М, а на 2/3 - ионно-ковалентными связями M-X. Этот впервые полученный результат (по оценки параметров f_m кристаллов) представляет несомненный интерес для теоретической кристаллохимии, поскольку подобные данные не отражены в современных учебниках, руководствах и справочниках (Бокий, 1971; Урусов, 1975; 1987). В то же время можно привести примеры практического использования найденных параметров f_m для объяснения некоторых свойств сульфидов и их аналогов. Известно, что такие кристаллы, как сульфиды, селениды и теллуриды серебра и меди (Cu₂S, Ag₂S, Ag₂Se и др.) в той или иной степени обладают ковкостью, режутся, что естественно связать с высокими величинами параметров металлической связи (f_m ≈ 0,5), т. е. эти кристаллические соединения являются наполовину металлами. А в таких минералах, как домейкит Cu₃As (f_m = 0,78) и дискразит Ag₃Sb (f_m = 0,85) доля металлических связей преобладает над вкладом ионно-ковалентных. Учитывая величины параметров f_m, можно успешно решать некоторые кристаллохимические задачи, например, объяснять парадоксы твердости минералов. Так, например, известно, что в рядах изоструктурных и изоэлектронных кристаллов MgS→CaS→SrS→BaS, ZnS→CdS→HgS твердость закономерно падает, что естественным образом объясняется (Поваренных, 1963) ростом размеров катионов (и межатомных расстояний) по мере опускания вниз в пределах соответствующих групп Периодической системы. Следовательно, в ряду изоэлектронных и изоструктурных (тип пирита) кристаллов FeS₂→RuS₂→OsS₂ твердость должна падать. Однако на самом деле твердость в этом ряду сначала неожиданным образом довольно резко растет (от пирита FeS₂ к лауриту RuS₂), а затем падает (от лаурита RuS₂ к эрликманиту OsS₂), что не согласуется с результатами оценок по кристаллохимическим формулам твердости (Поваренных, 1963): Н_М(FeS₂) = 6,7, Н_М(RuS₂) = Н_М(OsS₂) = 6,3. Фактически наблюдаемый ход изменения твердости минералов в этом ряду, как показали расчеты (таблица 1.28), находит объяснение в вариации доли металлических связей: в пирите два электрона металла (Fe) участвуют в металлических связях, а в лаурите и эрликманите - четыре электрона. Это связано с тем, что у менее электроотрицательных, чем Fe, атомов Ru и Os сравнительно легко отщепляются два дополнительных электрона для участия в связях M-M. Учет этого обстоятельства в соответствующих расчетах параметров W, W_v и Н_М приводит к согласию расчетных и экспериментальных значений твердости в рассматриваемом ряду минералов: Н_М(FeS₂)<Н_М(RuS₂)>Н_М(OsS₂). Именно такой ход изменения твердости минералов в этом ряду косвенно подтверждается аналогичным ходом изменения энергоплотностей: E_v(FeS₂) = 47 кДж/см³, E_v(RuS₂) = 55 кДж/см³, E_v(OsS₂) = 51 кДж/см³ (Зуев, Денисов, Мочалов и др., 2000). Убедительное доказательство необходимости учета металлических связей для объяснения наблюдаемой твердости следует из рассмотрения двух других обладающих структурой пирита минералов - мичнерита PdBi₂ и ауростибита AuSb₂. Для мичнерита в случае принятия остовной формулы [Pd⁽⁴⁺²⁾⁺][Bi⁴⁺]₂ расчеты дают W = 45,9 МДж/моль, f_m = 0,33, W_v = 0,83 МДж/см³ и Н_М = 2,9 (экспериментальная твердость около 3). Для ауростибита приходится допустить следующий остовный состав - [Au⁽⁴⁺³⁾⁺][Sb⁴⁺]₂, который приводит к следующим параметрам этого минерала: W = 51,43 МДж/моль, f_m = 0,43, W_v = 1,18 МДж/см3 и Н_М = 4,1. Последняя величина практически совпадает со справочной твердостью ауростибита 3,75-4,2 согласно (Поваренных, 1965). Обращает на себя внимание следующая, требующая объяснения закономерность. Если в простых бинарных сульфидах без примеси металлических связей сера шестивалентна (таблицы 1.23-1.25), то в сложных сульфидах тяжелых переходных металлов с примесью металлических связей сера, как правило, находится в четырехвалентном состоянии, т. е. в виде остовов [S⁴⁺] (таблица 1.28). Наиболее простое и естественное объяснение заключается в том, что с энергетической точки зрения легче отщепить дополнительные «металлические» электроны от переходного металла, чем превратить остов [S⁴⁺] в остов [S⁶⁺]. Последний процесс требует больших энергетических затрат и поэтому менее вероятен. Таким образом, здесь можно говорить о своеобразной конкурентной борьбе между атомами за определенный энергетический выигрыш при образовании химических связей. Проблема вклада металлического взаимодействия в общую твердость рассматриваемой группы сульфидов и их аналогов имеет принципиальное значение. Дело в том, что в кристаллохимической теории твердости А. С. Поваренных этот важный аспект просто упущен. Более того, согласно трактовке А. С. Поваренных, в галените, например, неподеленные пары 6s²-электронов у атомов Pb является разрыхляющими, ослабляющими связи Pb-S и соответственно уменьшающими твердость минерала[1], что, по нашим данным, принципиально не верно. На самом деле, как было показано, эти пары электронов делокализованы между атомами Pb[2] и дополнительно стабилизируют решетку галенита, внося свой вклад в виде компоненты Н_Мm в общую твердость минерала. С позиций учета металлических связей приведем пример объяснения различия свойств полиморфных модификаций на примере пары «киноварь-метациннабарит» с общей формулой HgS. Киноварь обладает квазикоординационной цепной структурой, минерал красного цвета с алмазным до металловидного блеском, в некоторых минералогических справочниках указывается, что киноварь частично режется, т. е. налицо признаки металлических свойств. Для их отражения предлагается остовная модель [Hg⁽²⁺²⁾⁺][S²⁺], для которой W = 22,08 МДж/моль, f_m = 0,34, W_v = 0,77 МДж/моль и Н_М = 2,7 в полном согласии со справочной твердостью киновари. Метациннабарит обладает координационной решеткой типа сфалерита, минерал черного цвета, хрупок и заметно тверже киновари. Для остовного состава [Hg²⁺][S⁶⁺] получаются следующие параметры: W = 29,88 МДж/моль, f_m = 0, W_v = 0,99 МДж/см³, Н_М = 3,5, что соответствует справочной твердости метациннабарита (Поваренных, 1965). Разумеется, металлические связи могут присутствовать не только в сульфидах и их аналогах, но также и в других классах кристаллических соединений - оксидах, карбидах, нитридах, фосфидах и боридах переходных металлов. Например, по соответствию расчетной и экспериментальной твердости куприта Cu₂O (Н_М = 4) можно заключить, что в этом минерале имеется определенная доля металлической связи (f_m = 0,28), при этом допускается участие приблизительно 1,5 электрона у атома Cu во взаимодействии Cu-Cu. Соответствующая остовная формула куприта - [Cu^(1+1.5)+]₂[O⁴⁺] с параметрами W = 27,53 МДж/моль, W_v = 1,17 МДж/см³ и Н_М = 4,1. Другие альтернативные варианты для куприта без связей Cu-Cu, выражаемые остовными формулами [Cu⁺]₂[O⁴⁺] или [Cu⁺]₂[O⁶⁺], не соответствуют твердости куприта (первая из них резко занижает твердость, а вторая завышает ее). Для изоструктурного с купритом кристалла Ag₂O рекомендуется остовная формула [Ag⁽¹⁺²⁾⁺]₂[O⁴⁺], соответствующие параметры: E_α = 0,85 МДж/моль, W = 30,65 МДж/моль, W_m = 0,13 МДж/г, W_v = 0,94 МДж/см³, Н_М = 3,3 (эксперимент 3,5), f_m = 0,35. Характерными примерами других оксидов с металлическими связями являются кубические кристаллы NbO и TiO. В оксиде NbO формально двухвалентные атомы ниобия имеют КЧ = 4(O) + 8(Nb) и образуют ОЦК-подрешетку (Земан, 1969). В моноксиде титана TiO формально двухвалентные атомы титана имеют КЧ = 6(O) + 12(Ti) и образуют ГЦК-подрешетку. Оба кристалла непрозрачны, обладают черным цветом с металловидным блеском, хорошие проводники, довольно твердые (Н_М ≈ 7,5). Для первого из них предлагается следующая, учитывающая металлическую компоненту связи остовная модель - [Nb⁽²⁺³⁾⁺][O⁴⁺], для которой расчеты дают W = 31,88 МДж/моль, f_m = 0,35, W_v = 2,12 МДж/см³ и Н_М = 7,4. Соответствующие данные для кристалла TiO - [Ti⁽²⁺²⁾⁺][O⁴⁺], W = 27,51 МДж/моль, f_m = 0,25, W_v = 2,13 МДж/см³ и Н_М = 7,5. В металловидных карбидах типа Fe₃C, WC, VC, NbC, TaC присутствие металлических связей M-M не вызывает сомнений, примеры некоторых таких соединений приведены в конце таблицы 1.28. 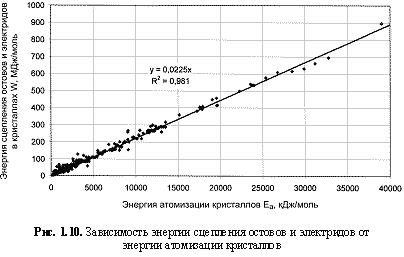В расчетах по формуле (1.16) энергетических параметров W использовались величины Е_α из (Зуев, Мочалов, Денисов и др., 2000). Однако совершенно очевидно, что между этими параметрами должна существовать взаимосвязь, поскольку оба параметра характеризуют термодинамическую и механическую стабильность соединений. Попытка построить соответствующую зависимость для более 350 минералов и других кристаллических соединений (рис. 1.10) привела к следующей простой эмпирической формуле (в которой оба параметра выражаются в МДж/моль):

W = 22,5E_α.                                                                     (1.22)

Комбинируя эту формулу с формулой (1.16), получаем W = ΣI_n + E_α = 22,5E_α, откуда 22,5E_α - E_α = 21,5E_α = ΣI_n и далее

E_α = ΣI_n/21,5 = 0,0465ΣI_n.                     (1.23)

Подставляя это выражение в формулу (1.16), имеем W = ΣI_n + 0,0465ΣI_n и окончательно:

W = 1,0465ΣI_n.                               (1.24)

Таким образом, пользуясь этой формулой, можно оценивать энергию сцепления остовов и связующих электронов соединения по потенциалам ионизации атомов, если, разумеется, известен его остовный состав. При этом знание параметра энергии атомизации соединения не требуется, поскольку этот важный параметр в отсутствии экспериментальных данных может быть оценен по формуле (1.23). В частности, для кристалла Na₂O расчет энергии атомизации по этой формуле дает почти точное соответствие с экспериментальной величиной 0,879 МДж/моль. Опробирование формулы (1.23) на 68 сложных оксидных и силикатных минералах (включая пироксены, амфиболы, слюды и т. д.) при условии принятия в них остовов [O⁴⁺] дало очень хорошие результаты: среднее расхождение между расчетными и экспериментальными энергиями атомизации составило около 2% (таблица 1.29). Другие примеры даны в таблице 1.30, из которой следует также вполне удовлетворительная сходимость расчетных и экспериментальных (рассчитанных из термохимических данных) энергий атомизации. Понятно, что, располагая известными (экспериментальными) величинами Е_α с использованием формулы (1.23), возможно решение обратной задачи нахождения зарядов атомных остовов в соединениях подобно тому, как это было продемонстрировано по критерию твердости в таблицах 1.15-1.21. Таким образом, данные таблицы 1.29 можно рассматривать в качестве энергетического обоснования принятых остовных составов сложных минералов (для катионов это [Na⁺], [Mg²⁺], [Al³⁺], [Si⁴⁺], [H⁺] и др. c обычными для них валентностями, для анионов [O⁴⁺], [F³⁺]). Принятие для анионных компонентов других валентных состояний приводит к резкому расхождению расчетных и экспериментальных величин энергии атомизации (росту параметров ΔЕ_α,% в таблице 1.29). Для подтверждения приведем следующие примеры. В случае периклаза MgO расчеты по формуле (1.23) дают: Е_α = 0,32 МДж/моль для остовного варианта [Mg²⁺][O²⁺], Е_α = 0,914 МДж/моль для варианта [Mg²⁺][O⁴⁺] и Е_α = 2,045 МДж/моль для варианта [Mg²⁺][O⁶⁺]. Экспериментальная энергия атомизации периклаза Е_α = 0,998 МДж/моль, поэтому выбор второго варианта с четырехвалентным кислородом однозначен. Напомним, что тот же самый результат был получен по критерию твердости (таблица 1.19). Для манганозита MnO в предположении остовного состава [Mn²⁺][O⁴⁺] ΣI_n = 19,7 МДж/моль, и расчетная величина Е_α по формуле (1.23) составит 0,916 МДж/моль в полном согласии с экспериментальной величиной Е_α = 0,915 МДж/моль. Для перманганата калия K[MnO₄] хорошее согласие экспериментальной энергии атомизации (Е_α = 2,18 МДж/моль) и рассчитываемой по формуле (1.23) Е_α = 2,23 МДж/моль получается в случае принятия остовов [K⁺][Mn⁷⁺][O²⁺]₄ (ΣI_n = 47,94 МДж/моль). Заметим, что в этом кристалле кислород двухвалентен в отличие от четырехвалентного состояния в силикатах (таблица 1.29). Таблица 1.29 Расчет энергии атомизации сложных кислородсодержащих минералов по формуле (1.23) в сопоставлении с экспериментальными данными

Минерал	Формула	ΣIn,МДж/моль	Еα,МДж/мольрасчет	Еα,МДж/мольэксперим.	ΔЕα,%
Тальк	Mg3Si4O10(OH)2	258,65	12,03	11,65	+3,3
Фенакит	Be2SiO4	85,15	3,96	4,26	-7,0
Альбит	NaAlSi3O8	175,26	8,15	7,70	+5,8
Анортит	CaAl2Si2O8	171,68	7,98	7,95	+0,4
Глаукофан	Na2Mg3Al2Si8O22(OH)2	519,38	24,16	23,45	+3,0
Форстерит	Mg2SiO4	84,21	3,92	3,93	-0,3
Фаялит	Fe2SiO4	84,48	3,93	3,78	+4,0
Каолин	Al2Si2O5(OH)4	192,67	8,96	8,82	+1,6
Энстатит	MgSiO3	64,55	3,33	2,91	+3,2
Сфен	CaTiSiO5	107,84	5,01	4,96	+1,1
Клинохлор	Mg5Al2Si3O10(OH)8	376,05	17,49	17,85	-2,0
Шпинель	MgAl2O4	82,35	3,83	4,09	-6,4
Антофиллит	Mg7Si8O22(OH)2	516,86	24,04	23,28	+3,3
Серпентин	Mg6Si4O10(OH)8	377,92	17,58	17,64	-0,3
Силлиманит	Al2SiO5	107,59	5,00	4,95	+1,0
Кианит	Al2SiO5	107,59	5,0	4,96	+0,9
Турмалин (дравит)	NaMg3Al6Si6O18(BO3)3(OH)4	665,13	30,94	31,04	-0,3
Мусковит	KAl2[AlSi3O10](OH)2	257,97	12,00	11,89	+0,9
Флогопит	KMg3[AlSi3O10](OH)2	254,26	11,83	11,94	-0,9
Биотит	KFe3[AlSi3O10](OH)2	254,65	11,84	11,66	+1,6
Микроклин	KAlSi3O8	175,18	8,15	7,79	+4,6
Берилл	Be3Al2Si6O18	392,44	18,25	17,94	+1,7
Топаз	Al2SiO4F2	112,32	5,22	5,36	-2,6
Тремолит	Ca2Mg5Si8O22(OH)2	515,96	24,00	23,57	+1,8
Хлоритоид	FeAl2[SiO4]O(OH)2	147,47	6,87	6,93	-0,9
Торит	ThSiO4	86,29	4,01	4,2	-4,5
Тримерит	CaMn2Be3[SiO4]3	253,67	11,8	12,24	-3,6
Синхалит	MgAl[BO4]	84,1	3,91	4,15	-5,8
Гроссуляр	Ca3Al2Si3O12	254,99	11,86	12,22	-2,9
Альмандин	Fe3Al2Si3O12	256,75	11,94	11,57	+3,2
Андрадит	Ca3Fe2Si3O12	255,27	11,87	11,54	+2,9
Акерманит	Ca2MgSi2O7	147,86	6,88	7,08	-2,8
Геленит	Ca2Al2SiO7	146,0	6,79	7,2	-5,7
Геденбергит	CaFeSi2O6	128,79	5,99	5,87	+2,0
Диопсид	CaMgSi2O6	128,65	5,98	5,96	+0,3
Жадеит	NaAlSi2O6	130,37	6,06	6,00	+1,0
Еремеевит	Al6[BO3]5(OH)3	383,69	17,85	18,73	-4,7
Зуньит	Al12[AlSi4O16][SiO4](OH)18Cl	823,16	38,29	38,19	+0,3
Берилсодалит	Na4[BeAlSi4O12]Cl	278,31	12,94	12,82	+1
Монтморил-лонит	Na0.33Al2[Al0.33Si3.67O10](OH)2	260,94	12,14	11,93	+1,8
Фторфлогопит	KMg3[AlSi3O10]F2	238,9	11,11	11,23	-1,1
Лепидолит	KLi1.5Al1.5[AlSi3O10](OH)2	256,17	11,92	11,44	+4,1
Аксинит	Ca2(Mn,Fe)Al2[BO3][Si4O12](OH)	343,52	15,98	16,16	-1,1
Джимбоит	Mn3[BO3]2	125,28	5,83	5,93	-1,8
Апофиллит	KCa4[Si4O10]2F×8H2O	608,26	28,29	28,18	+0,4
Нонтронит	NaFe2[AlSi3O10](OH)2×4H2O	337,22	15,68	15,45	+1,5
Томсонит	NaCa2[Al5Si5O20]×6H2O	549,42	25,55	26,36	-3,1
Бирюза	CuAl6[PO4]4(OH)8	531,63	24,73	24,67	+0,2
Сколецит	Ca[Al2Si3O10]	276,87	12,88	12,83	+0,4
Шамозит	Fe5Al2Si3O10(OH)8	376,72	17,52	17,43	+0,5
Везувиан	Ca19Mg3Al10[Si2O7]4[SiO4]10O2´ (OH)6	1610,5	74,91	74,69	+0,3
Корнерупин	Mg5Al8[SiO4]5[BO3]O5(OH)	616,68	28,68	28,08	+2,1
Филлипсит	KCa[Al3Si5O16]×6H2O	467,44	21,74	21,83	-0,4
Гидроталькит	Mg6Al2(OH)16[CO3]×4H2O	471,02	21,91	23,06	-5,0
Пироаурит	Mg6Fe2(OH)16[CO3]×4H2O	471,3	21,92	22,38	-2,1
Власовит	Na2ZrSi4O11	240,44	11,18	10,79	+3,6
Тиллеит	Ca5[Si2O7][CO3]2	284,26	13,22	12,87	+2,7
Амезит	Mg4Al2[Al2Si2O10](OH)8	374,19	17,4	17,99	-3,3
Цельзиан	BaAl2Si2O8	171,42	7,97	8,02	-0,6
Грюнерит	Fe7[Si8O22](OH)2	506,79	23,57	22,68	+3,9
Ильваит	CaFe2Fe[Si2O7]O(OH)	190,11	8,84	8,52	+3,8
Людвигит	Mg2Fe[BO3]O2	103,9	4,83	4,85	-0,4
Мейонит	Ca4[AlSiO4]6[CO3]	583,49	27,14	26,74	+1,5
Морденит	Na2Ca[AlSi5O12]4×6H2O	1181,5	54,95	52,43	+4,8
Пренит	Ca2Al[AlSi3O10](OH)2	255,88	11,9	12,04	-1,2
Пумпеллит	Ca4MgAl5Si6O21(OH)7	586,43	27,28	28,47	-4,2
Сепиолит	Mg4[Si6O15](OH)2×6H2O	477,47	22,21	22,3	-0,4
Ставролит	Fe2Al9Si4O23(OH)	511,33	23,78	23,86	-0,3

Таблица 1.30 Расчетные величины энергии атомизации и относительной твердости некоторых кристаллических моноксидов и моносульфидов переходных металлов 4а-периода Периодической системы в сопоставлении с соответствующими экспериментальными данными

Кристалл	Образующие кристаллическую решетку остовы	ΣIn, МДж/моль*	Еα,МДж/моль		W,МДж/моль	Wv,МДж/см3	Относительная твердость НМ
			Расчет по (1.23)	Экспе-римент			Расчет по (1.20)	Эксперимент
TiO	[Ti(2+2)+][O4+]	26,27	1,22	1,24	27,51	2,13	7,5	7,0-7,5
VO	[V(2+2)+][O4+]	26,87	1,25	1,20	28,07	2,40	8,5	7,5-8,0
CrO	[Cr2+][O4+]	19,72	0,92	1,04	20,76	1,65	5,8	6,0
MnO	[Mn2+][O4+]	19,70	0,92	0,914	20,61	1,56	5,5	5,5
FeO	[Fe2+][O4+]	19,79	0,92	0,94	20,73	1,73	6,1	5,5-6,0
CoO	[Co2+][O4+]	19,88	0,92	0,92	20,80	1,58	5,5	5,5
NiO	[Ni2+][O4+]	19,96	0,93	0,92	20,88	1,90	6,7	6,0-7,0
TiS	[Ti(2+2)+][S4+]	19,97	0,93	1,01	20,98	1,08	3,8	4,0
CrS	[Cr(2+2)+][S4+]	21,15	0,98	0,85	22,00	1,27	4,4	4,5

^* - сумма потенциалов ионизации.

ПРИМЕЧАНИЕ. Кристаллы TiO, VO, CrO, MnO, FeO, CoO, NiO имеют структуру типа NaCl, кристаллы TiS и CrS - структуру типа NiAs. Параметры W получены суммированием величин ΣI_n и экспериментальных энергий атомизации Е_α. Корректность принятого электронного строения и энергетических параметров рассмотренных в таблице кристаллических соединений можно дополнить критерием близости расчетных и экспериментальных величин максимальных частот колебаний атомов. Ниже приведены некоторые соответствующие данные, полученные по формуле (1.21) в сопоставлении с экспериментальными (Мамыров, 1991), помещенными в скобках после расчетных: TiO - n_m == 11,06 (12,4) ТГц, MnO - n_m = 8,53 (9,91) ТГц, TiS - n_m = 7,93 (8,54) ТГц, CrS - n_m = 7,93 (8,17) ТГц. В качестве еще одного очень интересного примера определим истинную валентность железа в комплексе [Fe(CN)₆]^-4, а точнее в кристалле K₄[Fe(CN)₆]×3H₂O. По этому вопросу есть две точки зрения. Если принять в комплексе ординарными все железо-углеродные связи (Fe-C≡N), то железо двухвалентно, как указывается во всех спра­вочниках по химии, где это соединение называется гексаферратом (II) калия. Если же принять использование в связях всех восьми валентных электронов железа, то железо-углеродные связи окажутся по Полингу полуторными (Pauling, 1960). Для первого варианта с остовами [K⁺]₄[Fe²⁺][C⁴⁺]₆[N³⁺]₆[H⁺]₆[O⁴⁺]₃ сумма потенциалов ионизации атомов до состояния остовов ΣI_n = 203 МДж/моль, Е_α = 9,44 МДж/моль. Для второго варианта с остовами [K⁺]₄[Fe⁸⁺][C4⁺]₆]N³⁺]₆[H⁺]₆[O⁴⁺]₃  ΣI_n = 254,744 МДж/моль и Е_α = 11,85 МДж/моль. Экспериментальная величина энергии атомизации кристалла Е_α = 11,44 МДж/моль. Для последнего (второго) варианта разница между расчетной и экспериментальной энергией атомизации ΔЕ_α = +3,6%, а для варианта с двухвалентным железом ΔЕ_α = -17,5%. Следовательно, вариант с восьми­валентным железом в кристалле K₄[Fe(CN)₆]×3H₂O явно предпочтительнее. Приведенный пример заслуживает внимания, поскольку свидетельствует о том, что несовпадение формальной (классической) и фактической (электронной) валентности возможно не только для анионных, но также и для катионных компонентов кристаллических соединений (см. также таблицу 1.28). Моноксиды переходных металлов в таблице 1.30 расположены сверху вниз в порядке роста атомного номера катиона. Кристаллы этого ряда подразделяются на две группы: первую из двух кристаллов TiO и VO с металлическими связями (f_m = 0,24-0,25) и вторую из всех остальных кристаллов без металлических связей, что соответствующим образом отражено в зарядах остовов катионов. Это деление четко коррелируется величинами двух параметров - энергией атомизации и относительной твердостью. У кристаллов второй группы энергии атомизации довольно близки (0,9-1,0 МДж/моль) и заметно меньше (на 25-30%) энергий атомизации у кристаллов первой группы, что связано у них с дополнительным взаимодействием M-M и отсутствием такового в моноксидах без связей M-M. Соответственно, твердость кристаллов TiO и VO заметно выше, чем у кристаллов второй группы, где она приблизительно одинакова. В моносульфидах переходных металлов TiS и CrS, обладающих структурами типа NiAs, однозначно присутствие металлических связей в большем (нежели в соответствующих оксидах) количестве: f_m(TiS) = 0,33 и f_m(CrS) = 0,35. В качестве интересного вывода из материалов данного раздела (см. таблицы 1.19, 1.21) следует теоретическая возможность - при соответствующем возбуждении валентности кислорода (O^IV→O^VI или [O⁴⁺]→[O⁶⁺]) и вовлечении в химическую связь 2s²-электронов - кристаллов типа MgO, Mg₂SiO₄ с близкой к алмазу твердостью. Более того, как показывают расчеты, в случае реализации в кристалле корунда Al₂O₃ остовов [Al³⁺], [O⁶⁺] и двухэлектронных связей Al-O[1] его твердость была бы выше алмаза, а энергия атомизации в два раза выше справочной (таблица 1.31). Однако для получения таких кристаллических соединений на практике потребовались бы очень высокие величины температуры и давления (порядка 100 ГПа).

В заключение можно констатировать, что материалы данного раздела аргументированно, на наш взгляд, демонстрируют возможность использования энергии сцепления остовов и связующих электронов для решения двух кристаллохимических проблем: определения истинных валентных состояний атомов и количественной оценки долей металлического межатомного взаимодействия в кристаллах, если оно объективно присутствует в них и влияет на свойства. Два других энергетического подхода - энергия атомизации и энергия кристаллической решетки - не дают такой возможности. И если в энергии атомизации энергия металлического взаимодействия в соответствующих гетероатомных кристаллах присутствует в скрытом, неподдающимся количественной оценке виде, то в энергии кристаллической решетки энергия металлической связи вообще не фигурирует. Немаловажно также и то обстоятельство, что разработанный метод описания электронного строения, свойств (твердости) и оценки доли металлической связи применим к соединениям любой степени сложности, для которых соответствующие строгие квантово-химические расчеты с вытекающими из них свойствами сложных кристаллов до сих пор просто не реальны.

Таблица 1.31 Варианты остовно-электронных моделей корунда Al₂O₃ в сопоставлении с расчетными твердостью (экспериментальная твердость корунда Н_М = 9) и энергией атомизации (справочная величина Е_α = 3,074 МДж/моль)

Варианты остовов	q(Al-O),e-	W,МДж/моль	Wv,МДж/см3	НМ	Еα,МДж/моль
[Al3+]2[O2+]3	1,0	25,54	1,0	3,5	1, 13
[Al3+]2[O4+]3	1,5	65,68	2,575	9,0	2,92
[Al3+]2[O6+]3	2,0	142,10	5,57	>15	6,31

ПРИМЕЧАНИЕ. Параметры W и Н_М получены по формулам (1.20), а Е_α по формуле (1.23). Несомненно, заслуживает внимания также возможность удовлетворительной оценки энергии атомизации сложных кислород содержащих минералов (силикатов и др.) с использованием лишь потенциалов ионизации атомов (формула (1.23), таблица 1.29). Разумеется, это возможно при условии корректного определения остовно-электронного состава соединений, чему и был посвящен данный раздел. Как следует из материалов данного раздела, корректную оценку валентных состояний атомов в кристаллических соединениях с использованием соответствующих энергетических расчетов можно произвести по критериям физических свойств (относительной твердости, частотам колебаний атомов) и по энергии атомизации. Еще раз подчеркнем, что до сих пор проблема определения истинных валентных состояний неметаллов в гетероатомных кристаллических соединениях в литературе практически не рассматривается. Впервые изложенные здесь рекомендуемые нами энергетические подходы преследую цель решения данной проблемы.

---

[1] Согласно остовно-электронной концепции строения кристаллов (Зуев, 1990) валентность атома в соединениях определяется зарядом его остова (валентность = заряду атомного остова = числу отдаваемых атомом электронов для участия в химических связях). [2] Фактически речь идет о наглядном кристаллохимическом моделировании представлений единой зонной теории твердых тел. [3] Иначе говоря, это энергия, которая выделяется при рекомбинации электронов атомными остовами в результате превращении их в свободные нейтральные составляющие атомы. [4] Энергии (потенциалы) ионизации атомов взяты из справочника (Эмсли, 1993), а энергии атомизации соединений из книги (Зуев, Денисов, Мочалов и др., 2000). [5] Впервые схемы с одноэлектронными связями М-Х в кристаллах NaCl и MgO были, по-видимому, предложены (без, однако, энергетического обоснования) в работах Сюше (Сюше, 1969). [6] Здесь необходимо уточнить, что в молекулярных оксидных кристаллах типа арсенолита As₂O₃, сенармонтита Sb₂O₃ и др. кислород, естественно, находится в двухвалентном состоянии, т. е. в виде остовов [O²⁺]. Это же валентное состояние кислорода наблюдается и, по нашим расчетам, в некоторых комплексных кристаллических соединениях c ярко выраженным островным мотивом структуры, например, в нитратах (см. табл. 1.22). [7]Имеются в виду сульфиды непереходных металлов, в сульфидах же тяжелых переходных металлов с примесью металлических связей чаще всего реализуются остовы [S⁴⁺]. [8] А. С. Поваренных ввел соответствующий коэффициент ослабления связей β<1 (Поваренных, 1963, с. 113). [9] Атомы Pb в галените образуют ГЦК решетку с КЧ(Pb) = 12(Pb) и d(Pb-Pb) = 4,186 Å. [10] Именно такая трактовка конституции корунда встречается в некоторых предыдущих работах, включая и наши (Зуев, 1990). С точки зрения энергии сцепления атомных остовов и связующих электронов это не соответствует экспериментальной твердости корунда (около 9) и справочной энергии атомизации. Решетка корунда построена, по-видимому, из атомных остовов [Al³⁺] и [O⁴⁺].