2.1. Зависимость физических свойств минералов и неорганических кристаллов от структурной рыхлости

Средний грамм-атомный объем кристаллического вещества в качестве показателя его термодинамической стабильности или параметр структурной рыхлости минералов, имеющий размерность см3/г-ат, вычисляется (Евзикова и Ициксон, 1969; Евзикова, 2001) по формуле:

ω = M/(nρ);                                                                                     (2.1)

где М - молекулярная масса, равная сумме атомных весов элементов соединения, n - число структурных узлов (атомов, ионов, комплексов или радикалов) в формульной единице соединения, ρ - его плотность. В случае гомоатомных кристаллических соединений, образованных атомами одного сорта, этот параметр вычисляется по более простой формуле ω = A/ρ (A - атомный вес элемента). Естественно, возникает вопрос, насколько физически оправдано представление о вычисляемом по формуле (2.1) некотором среднем грамм-атомном объеме вещества в случае гетероатомных кристаллов? Здесь уместно напомнить, что реальные размеры (радиусы) атомов в большинстве таких кристаллов (минералов) с преобладающей в них промежуточной ионно-ковалентной связью оказываются близкими, т. е. формула (2.1) может вполне адекватно характеризовать структурную рыхлость именно сложных гетероатомных соединений. В данном разделе будет продемонстрирован другой немаловажный аспект прикладного использования структурной рыхлости минералов, отраженный в названии раздела. Теоретические предпосылки применения параметров ω минералов для описания их свойств заключаются в следующем. Параметр ω косвенно характеризует энергию межатомного взаимодействия минерального вещества, а точнее - уплотнение, контрактацию (сжатие) слагающих это вещество атомов благодаря эффекту химической связи. Из общих теоретических соображений ясно, что чем прочнее химические межатомные связи и больше их энергия, тем более отчетливо проявляется эффект «стягивания» атомов в компактную кристаллическую решетку (структуру) и тем меньше будет соответствующая величина ее структурной рыхлости. И наоборот, чем слабее химические связи соединения и меньше их энергия, тем больше будет параметр его структурной рыхлости. В подтверждении приведем оценки w для двух, столь резко различающихся по свойствам (твердости и др.) минералов, как галит NaCl и алмаз C: w(NaCl) = 58,453/(2x2,16) = 13,53 см3/г-ат и ω(С) = 12,01/3,52 = 3,41 см³/г-ат. Таким образом, связь между параметром ω и стабильностью (термодинамической, механической) твердого тела обратная. 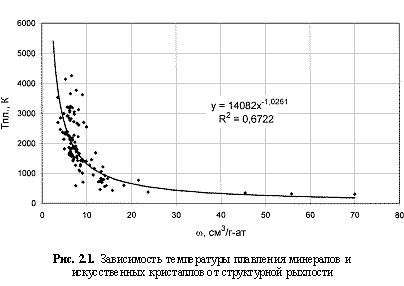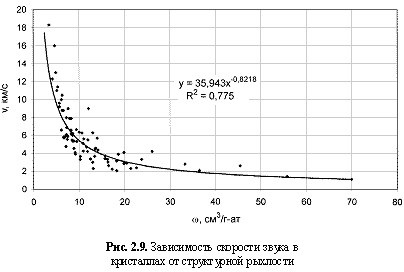Следовательно, если высказанное суждение справедливо, то, несомненно, должна существовать взаимосвязь структурной рыхлости веществ и их физических свойств. Соответствующие данные по физическим свойствам минералов и других кристаллических веществ заимствовались из статей (Yang, Parr, Uytterhoeven, 1987; Зуев, Мочалов, Щербатов, 1998; Муханов, 1998; Зуев, Аксенова, Мочалов и др., 1999), монографий (Поваренных, 1963, 1966; Юшкин, 1971; Мамыров, 1989, 1991; Сокольский, 1992; Зуев, 1995;) и справочников (Справочник физических констант горных пород, 1969; Бацанов, 1986; Фекличев, 1989; Петрофизика, 1992;), а для искусственных и, в частности, тугоплавких кристаллов из справочников (Свойства элементов, 1976; Самсонов, Винницкий, 1976; Физико-химические свойства окислов, 1978; Свойства, получение и применение тугоплавких соединений, 1986; Андриевский, Спивак, 1989; Эмсли, 1993; Свойства элементов, 1997). Построение соответствующих многочисленных корреляционных зависимостей полностью подтвердило тезис о возможности удовлетворительной оценки самых различных свойств минералов и других неорганических кристаллов по параметрам структурной рыхлости. Привлекательной стороной параметра w является его простота, четкий вышеохарактеризованный физический смысл и возможность применения к кристаллическим соединениям любой сложности состава и структуры. Учитывая все сказанное, наряду с тремя другими энергетическими подходами, концепция структурной рыхлости минералов может рассматриваться в качестве альтернативного энергетического подхода к оценке физических свойств кристаллических веществ, и на основе выявленных корреляционных зависимостей «структурная рыхлость/физическое свойство» (примеры которых приведены на рис. 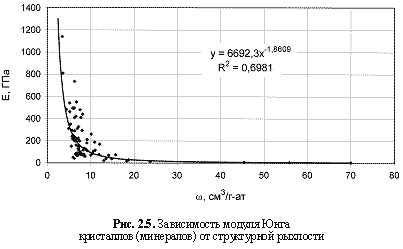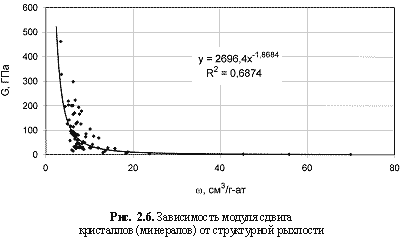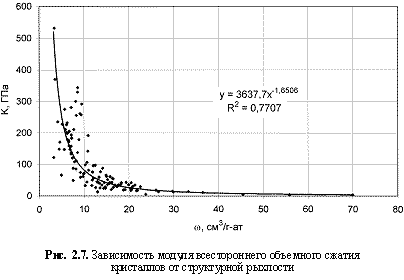2.1-2.12) были выведены формулы оценки следующих свойств минералов (неорганических кристаллов) по параметрам ω: - температуры плавления (Т_пл., К), относительной твердости по 15-балльной шкале (Н_М), абсолютной твердости (микротвердости) по Викерсу (HV, кгс/мм²), поверхностной энергии (E⁵_hkl, Дж/м²), модуля Юнга (Е, ГПа), модуля сдвига (G, ГПа), модуля всестороннего объемного сжатия (К, ГПа), коэффициентов теплового линейного (α_l, 10-6×К-1) и объемного (α_v, 10-6×К-1; α_v*, %) расширения, объемной сжимаемости (β, 10^-12×Па^-1), скорости распространения звука (ν, км/с), показателя преломления (n), трещинностойкости (К_1с, МПаxм^0.5), эффективной энергии разрушения (γ, Дж/м²), пограничной межатомной электронной плотности (ρ_min, e^-/ų), кристаллических электроотрицательностей (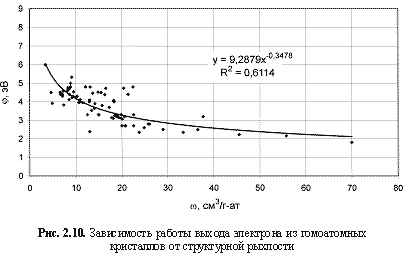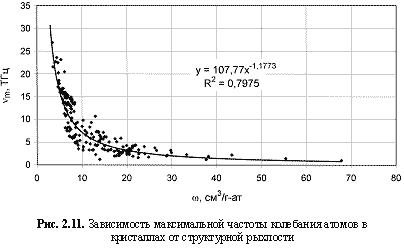ЭО_крист.) элементов, работы выхода электрона из гомоатомных кристаллов (φ, эВ), теплопроводности (λ, Вт/(мxК)), максимальных частот колебания атомов (ν_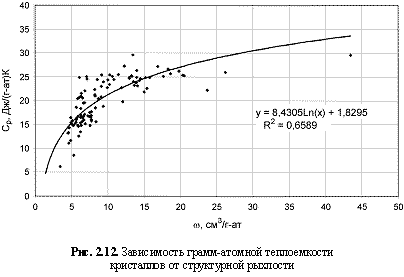m, ТГц), теплоемкости (C_p, Дж/(г-ат)К). Соответствующие формулы:

Т_пл.,К = 14082ω^-1.03;                         (2.2)

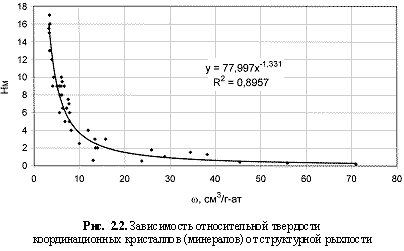
Н_М = 78ω^-1.33;                                       (2.3)

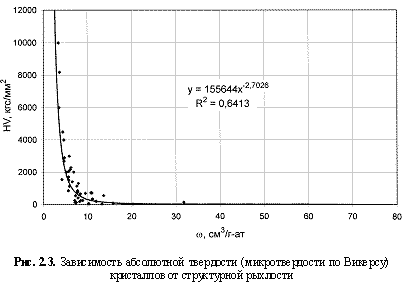
HV = 155644ω^-2.7;                                 (2.4)

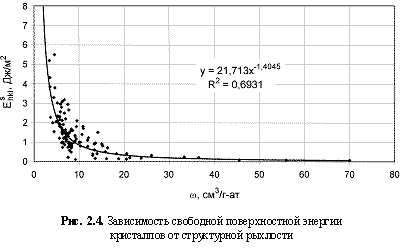
E_hs_kl = 21,7ω^-1.4;                                     (2.5)

Е = 6692,3ω^-1.86;                                   (2.6)

G = 2696,4ω^-1.87;                                   (2.7)

K = 3638ω^-1.65;                                      (2.8)

 

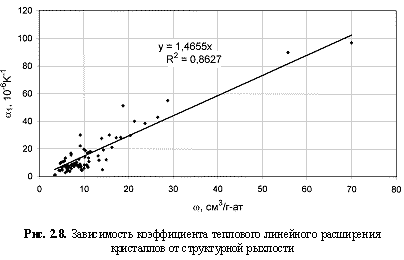
α_l = 1,4655ω;                                        (2.9)

α_v = 6,04ω;                                         (2.10)

α_v* = 0,0374ω;                                     (2.11)

β = 0,15ω² - 0,62ω;                            (2.12)

v = 36ω^-0.82;                                        (2.13)

n = 3ω^-0.33;                                          (2.14)

K_1c = 130,56ω^-2.26;                               (2.15)

γ = 1089,4ω^-2.4;                                   (2.16)

ρ_min = 2,59ω^-1.18;                                 (2.17)

ЭО_крист. = 4,5ω^-0.47;                             (2.18)

φ, эВ = 8,815ω^-0.32;                             (2.19)

λ = 5449,8ω^-3.831;                                (2.20)

v_m = 107,8ω^-1.18;                                  (2.21)

C_p = 8,43Ln(ω) + 1,83.                        (2.22)

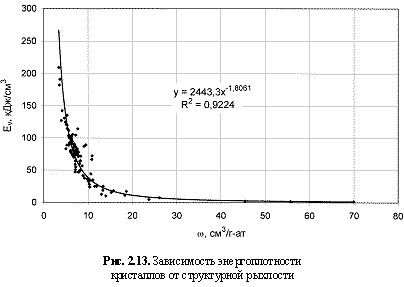
Таким образом, пользуясь одним единственным параметром вещества - структурной рыхлостью, можно давать (на основе выявленных зависимостей) количественные прогнозные оценки порядка 20 его физических свойств. Большинство этих зависимостей, как это следует из рис. 2.1-2.12, характеризуется довольно высокими величинами достоверности аппроксимации (средняя величина <R2> ≈ 0,70), т. е. дают вполне приемлемые результаты, часто не уступающие соответствующим данным, получаемым в рамках других энергетических подходов. Для увязки с последними были построены соответствующие зависимости (рис. 2.13-2.15) с вытекающими из них формулами:

E_v = 2443,3ω^-1.806;                              (2.23)

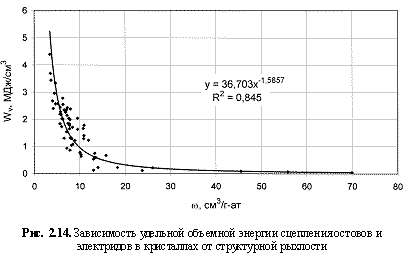
W_v = 36,76ω^-1.6;                                  (2.24)

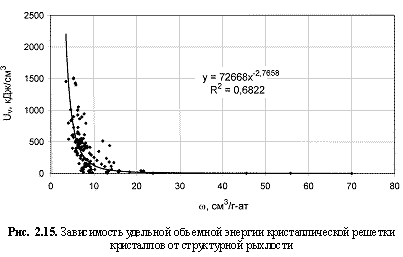
U_v = 72668ω^-2.766.                              (2.25)

В этих формулах E_v(кДж/см³) - энергоплотность кристалла, W_v(МДж/см³) - удельная объемная энергия сцепления остовов и электридов, U_v(кДж/см³) - удельная объемная энергия кристаллической решетки. Соответствующие обратные формулы для оценки структурной рыхлости по соответствующим величинам E_v,W_v и U_v будут следующими:

ω = 63,2E_v^-0.51;                                 (2.26)

ω = 9,51W_v^-0.53;                                (2.27)

ω = 30,7U_v^-0.25.                                (2.28)

Строго говоря, формула (2.3) применима для изодесмических координационных (а также каркасных) кристаллов. Однако с ее помощью можно вычислять также твердость анизодесмических комплексных кристаллических соединений, если входящие в их состав комплексы считать самостоятельными структурными узлами. Так, кристалл NaNO₃ можно рассматривать как бинарное соединение из ионов Na⁺ и [NO₃]^-. Тогда ω = 85,007/(2x2,27) = 18,72 см³/г-ат, и по формуле (2.2) Н_М = 1,6, что соответствует справочной твердости этого кристалла (1,5-2,0). Аналогичным образом для кристалла [NH₄]+[NO₃]^- ω = 80,014/(2x1,72) = 23,26 см³/г-ат и Н_М = 1,2 (эксперим. Н_М = 1,5). В случае кристалла K⁺[MnO₄]^- ω = (39,1 + 54,94 + 16x4)/(2x2,7) = 29,27 см³/г-ат и Н_М = 0,9 (эксперим. относительная твердость около 1). Для форстерита как комплексного кристалла Mg₂[SiO₄] ω= 140,7/(3x3,2) = 14,656 см³/г-ат и расчетная величина Н_М = 2,2, которая резко отличается от экспериментальной твердости форстерита (6,5-7). Если же считать форстерит сложным оксидом Mg₂SiO₄ (или 2MgOxSiO₂), то ω = 140,7/(7x3,2) = 6,28 см³/г-ат и расчетная твердость Н_М = 6,8 соответствует экспериментальной. Значит, форстерит лишь формально считается комплексным островным силикатом, а фактически по критерию твердости является сложным координационным оксидом типа шпинели MgAl₂O₄, для которой w = (24,305 + 27x2 + 16x4)/(7x3,6) = 5,65 см³/г-ат и Н_М = 7,8 (эксперим. 8). Впрочем, затронутые здесь вопросы детально и более корректно рассмотрены в рамках концепции энергии кристаллической решетки в разделе 2.2.1. Как показали соответствующие расчеты, использование параметров структурной рыхлости (по высокой величине R2 соответствующих зависимостей) рекомендуется при количественной оценки в первую очередь таких свойств кристаллов, как коэффициент теплового линейного расширения, эффективной энергии разрушения, работы выхода электрона из гомоатомных кристаллов, а также скорости звука. Для оценки других свойств кристаллов предпочтительнее использование дающих более корректные результаты альтернативных энергетических подходов, рассматриваемых в следующих разделах. Впрочем, сама возможность одновременного использования различных энергетических подходов к оценке одного и того же свойства кристалла заслуживает внимания - в плане возможности дополнительного контроля получаемых данных.