1.1. Структурная плотность кристаллических решеток твердых тел
Проблема структурной плотности кристаллических решеток как показателя условий минералообразования в свое время оживленно дискутировалась, соответствующий обзор приведен в работе (Евзикова и Ициксон, 1969), где авторами были предложены следующие параметры: η - число структурных единиц (атомов, молекул) в единице объема; Ω - абсолютная структурная рыхлость или объем, приходящийся в среднем на каждую структурную единицу минерала. Взаимосвязь этих параметров выражается формулой:
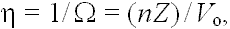 (1.1)
(1.1)
где: η - число структурных единиц в формуле минерала;
Z - число формульных единиц в элементарной ячейке, а
Vo - ее объем.
При всей очевидной ясности физического смысла параметров η и Ω необходимо указать на их недостаточность для характеристики структурной плотности минералов. Это фактически признается самими авторами в статье (Евзикова и Ициксон, 1969), где для реальных, практических оценок используется другая характеристика структурной рыхлости:
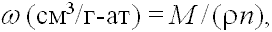 (1.2)
(1.2)
где:
М - молекулярная масса минерала (г/моль); ρ - плотность минерала (г/см3);
n - число атомов в формуле соединения.
[1]
Вопреки первоначальной негативной оценке (Наковник, 1972; Доливо-Добровольский, 1973), мы считаем эту характеристику минералов весьма ценной, и ее возможности в описании и предсказании свойств минералов будут продемонстрированы в соответствующем разделе.
Представляется очевидным, что по своему физическому смыслу параметр h должен быть одинаковым для решеток различных минералов, обладающих одним и тем же структурным типом. Однако в реальности это далеко не соблюдается, в чем легко убедиться при сравнении параметров η для группы кристаллов, обладающих решеткой типа галита (NaCl) - галенита (PbS) (таблица 1.1).
Таблица 1.1
Параметры η для кристаллов с решеткой типа NаCl-PbS
| Кристалл |
η |
Кристалл |
η |
Кристалл |
η |
| LiF |
0,122 |
NaF |
0,081 |
AgI |
0,036 |
| MgO |
0,107 |
MnS |
0,056 |
PbTe |
0,030 |
| FeO |
0,101 |
NaCl |
0,045 |
KI |
0,023 |
| MnO |
1,091 |
PbS |
0,038 |
RbI |
0,020 |
Крайние члены (первый и последний) в этой таблице различаются по параметру η более чем в 6 раз! Аналогичная картина имеет место при рассмотрении кристаллов других структурных типов. Следовательно, необходим другой, более корректный параметр структурной плотности, в качестве которого мы рекомендуем относительную структурную плотность кристаллической решетки - γ, который входит в новую кристаллохимическую формулу плотности минералов (Богданов и Зуев, 1991):
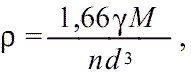 (1.3)
(1.3)
где 1,66 - константа, служащая для выражения плотности в г/см3, она равна атомной единице массы (а.е.м.) 1,66x10
-24 г, поделенной на коэффициент перевода кубических ангстремов в кубические сантиметры (1 Å = 10-8 см);
n - число атомов в формуле минерала;
d (Å) - параметр межатомных расстояний.
В случае сложных минералов в качестве параметра
d необходимо использовать усредненные для структуры величины межатомных расстояний. Например, для форстерита Mg
2[6]Si
[4]O
4[4], в котором
dср.(Mg-O
6) = 2,12 Å и
dср.(Si-O
4) = 1,63 Å, усреднение межатомных расстояний с учетом координационных чисел (
КЧ) атомов и их количеств в формуле минерала приводит к <
d> = (2,12x6x2 + 1,63x4x1)/16 = 2,0 Å.
Параметры γ определяются
КЧ атомов (см. рис. 1.1 и таблицу 1.2).
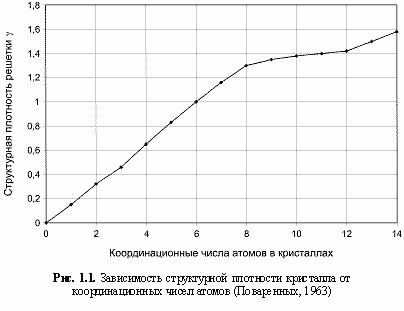
Таблица 1.2
Значения коэффициентов абсолютной и относительной плотности упаковки атомов в зависимости от их координационных чисел (Поваренных, 1963)
|
КЧ
|
v, % |
γ |
КЧ |
v, % |
γ |
КЧ |
v, % |
γ |
| 1 |
8,0 |
0,15 |
6 |
52,4* |
1,00 |
11 |
73,4 |
1,40 |
| 2 |
17,0 |
0,32 |
7 |
60,8 |
1,16 |
12 |
74,0* |
1,42 |
| 3 |
24,1(16,9*) |
0,46 |
8 |
68,0* |
1,30 |
13 |
- |
1,50 |
| 4 |
34,0* |
0,65 |
9 |
70,0 |
1,35 |
14 |
- |
1,58 |
| 5 |
43,5 |
0,83 |
10 |
72,3 |
1,38 |
|
|
|
Величины
v, % характеризуют степень заполнения пространства равновеликими шарами (атомами). Параметры γ получены делением рассчитанных (отмечены звездочками) и интерполированных (рис. 1.1) величин
v на величину
v = 52,4%, отвечающую
КЧ = 6 для структурного типа кристалла NaCl.
Однако можно вывести строгую формулу оценки g из кристаллохимических данных. Такую возможность дает сопоставление формулы (1.3) с известной рентгенометрической формулой плотности:
ρ= 1,66ZM / Vo (1.4)
Комбинируя эти две формулы, получим:
γ = Znd3 / Vo (1.5)
Расчет по формуле (1.5) для всех кристаллов (таблица 1.1) дает одинаковую структурную плотность γ = 1, что представляется вполне естественным, поскольку речь идет об одном и том же структурном типе кристаллов. Заметим, что формула (1.5) отличается от ранее предложенной формулы (1.1) лишь введением дополнительного параметра межатомных расстояний
d, т. е. фактически уточняет последнюю.
В таблице 1.3 приведены вычисленные по формуле (1.5) параметры γ для некоторых других распространенных структурных типов минералов.
Таблица 1.3
Параметры структурной плотности для некоторых распространенных структурных типов минералов
| Структурный тип |
γ |
Структурный тип |
γ |
|
NaCl, PbS
|
1,0 |
Cu2O (куприт)
|
0,49 |
|
CsCl, a-Fe
|
1,3 |
SiO2 (кварц)
|
0,33 |
|
Cu, Ag, Au
|
1,42 |
CaF2 (флюорит)
|
1,00 |
|
C (алмаз), ZnS
|
0,65 |
CaWO4 (шеелит)
|
0,85 |
|
FeS2 (пирит)
|
0,87 |
Ca3Al2Si3O12 (гранат)
|
0,88 |
|
FeS (троилит)
|
1,00 |
Mg2SiO4 (форстерит)
|
0,77 |
|
Al2O3 (корунд)
|
0,82 |
ZrSiO4 (циркон)
|
0,74 |
|
TiO2 (рутил)
|
0,72 |
CaTiO3 (перовскит)
|
1,31 |
|
PbCl2 (котунит)
|
1,15 |
Ca5[PO4]3F (апатит)
|
0,93 |
|
Al2SiO4F2 (топаз)
|
0,62 |
CaCO3 (кальцит)
|
0,65 |
|
Al2SiO5 (кианит)
|
0,65 |
CaCO3 (арагонит)
|
0,93 |
|
MgAl2O4 (шпинель)
|
0,78 |
BaSO4 (барит)
|
1,22 |
|
NaCaNb2O6F (пирохлор)
|
0,95 |
K2SO4 (арканит)
|
1,23 |
|
Fe2TiO5 (псевдобрукит)
|
0,70 |
Ba[NO3]2 (нитробарит)
|
0,87 |
|
YTiNbO6 (приорит)
|
0,84 |
CePO4 (монацит)
|
0,92 |
|
CaMn2O4 (марокит)
|
1,01 |
FeWO4 (вольфрамит)
|
0,75 |
|
La2O3
|
1,01 |
Cu2S (халькозин)
|
0,81 |
|
CuO (тенорит)
|
0,74 |
NiS (миллерит)
|
0,93 |
|
CaSO4 (ангидрит)
|
0,77 |
Na2SO4 (тенардит)
|
0,82 |
|
Ni3S2 (хизлевудит)
|
0,87 |
MgSiO3 (энстатит)
|
0,68 |
|
Co4[As4]3 (скуттерудит)
|
0,77 |
Mg7[Si8O22](OH)2 (антофиллит)
|
0,62 |
|
S8 (самородная сера)
|
0,34 |
Ca2Mg5[Si8O22](OH)2 (тремолит)
|
0,72 |
|
Se (селен цепной стр-ры)
|
0,46 |
Mg6[Si4O10](OH)8 (серпентин)
|
0,62 |
|
В (кристаллический бор)
|
0,76 |
Al2SiO5 (андалузит)
|
0,56 |
|
MoS2 (молибденит)
|
0,73 |
Al2SiO5 (силлиманит)
|
0,55 |
|
Hg2Cl2 (каломелит)
|
0,67 |
K2NiF4
|
1,1 |
|
BiF3 (Li3Bi)
|
1,60 |
MgCu2
|
1,69 |
|
Mn2O3 (биксбиит)
|
0,78 |
SnJ4
|
0,4 |
|
MoO3 (молибдит)
|
0,67 |
PbO (глет)
|
0,62 |
Согласно (Поваренных, 1963) (см. также таблицу 1.2), переход от γ к абсолютной плотности упаковки
v осуществляется по формуле:
v = 52,4γ, (1.6)
где 52,4 есть выраженная в % степень заполнения пространства равновеликими соприкасающимися атомами-шарами в решетке типа NaCl с октаэдрической координацией атомов. Поскольку из формулы (1.6) γ =
v / 52,4, то физический смысл параметра γ состоит в степени заполнения атомами пространства для рассматриваемого структурного типа по отношению к структурному типу NaCl. Соответственно параметр γ может быть охарактеризован как относительная структурная плотность решетки минерала.
Близким к параметру
v, согласно данным работы (Наковник, 1972), является так называемый упаковочный индекс
s (таблица 1.4).
Таблица 1.4
Сопоставление соответствующих параметров абсолютной плотности упаковки и упаковочных индексов в ряде минералов
| Минерал |
v, % |
s, % |
Минерал |
v, % |
s, % |
Минерал |
v, % |
s, % |
| Алмаз |
34 |
26 |
Жадеит |
42 |
49 |
Берндтит |
39 |
32 |
| Стишовит |
38 |
32 |
Алтаит |
52 |
53 |
Селлаит |
39 |
32 |
| Корунд |
43 |
45 |
Пирит |
46 |
50 |
Натролит |
27 |
33 |
| Мусковит |
43 |
42 |
Кварц |
17 |
21 |
Халькозин |
44 |
55 |
| Форстерит |
40 |
52 |
Тридимит |
14 |
19 |
Анальцим |
26 |
32 |
| Пироп |
47 |
46 |
Андалузит |
30 |
31 |
Торианит |
52 |
61 |
Рассмотренная концепция структурной плотности и способ нахождения параметра γ по формуле (1.5) относится, как отмечалось, к упаковкам равновеликих сфер. Однако эти данные можно распространять также и на катион-анионные упаковки разновеликих сфер, что следует из работы (Ye Danian, Zhang Jinmin, 1991). К тому же реальные, иначе называемые эффективными размеры катионных и анионных компонентов в гетероатомных минералах довольно близки, о чем свидетельствуют результаты соответствующих расчетов. Следует также оговориться, что формула (1.6) справедлива для упаковок из соприкасающихся сфер и следующих граничных условий 1,42 ≥ γ ≥ 0, где γ = 1,42 отвечает случаю плотнейших металлических упаковок с
КЧ = 12.
Итак, структурную плотность кристаллов можно выражать либо в виде относительной (γ), либо в виде абсолютной (
v) плотности упаковки атомов.
В качестве примеров в таблицах 1.5 и 1.6 приведены результаты оценок γ и
v по формулам (1.5) и (1.6) для ряда групп полиморфных модификаций минералов. Поскольку в таблице 1.5 в пределах каждой из групп минералов (модификаций) идентичного состава
КЧ атомов одинаковы, а межатомные расстояния М-Х довольно близки (Поваренных, 1966), то заметная разница в плотностях модификаций идентичного состава объясняется соответствующим различием плотностей упаковок (γ,
v), причем эта зависимость, естественно, симбатная. В таблицах 1.6 и 1.7 имеет место более радикальный рост r в зависимости от роста γ(
v), что связано с последовательным увеличением
КЧ катионов в рассматриваемом ряду кристаллов состава MgSiO
3 и SiO
2.
Таблица 1.5
Структурная плотность некоторых кристаллических модификаций минералов в сопоставлении с их плотностью
| Формула |
Название модификации |
γ |
v, % |
ρ, г/см3 |
|
SiO2
|
Коэсит
|
0,37 |
19,4 |
2,9 |
|
"
|
a-Кварц
|
0,33 |
17,3 |
2,65 |
|
"
|
b-Кварц
|
0,32 |
16,8 |
2,53 |
|
"
|
Кристобалит
|
0,29 |
15,1 |
2,3 |
|
"
|
Тридимит
|
0,275 |
14,4 |
2,2 |
|
"
|
Меланофлогит
|
0,25 |
13,1 |
2,0 |
|
TiO2
|
Рутил
|
0,72 |
37,7 |
4,3 |
|
"
|
Брукит
|
0,70 |
36,7 |
4,1 |
|
"
|
Анатаз
|
0,65 |
34,1 |
3,9 |
|
As2O3
|
Клодетит
|
0,38 |
19,9 |
4,2 |
|
"
|
Арсенолит
|
0,345 |
18,1 |
3,9 |
|
Sb2O3
|
Валентинит
|
0,48 |
25,2 |
5,8 |
|
"
|
Сенармонтит
|
0,46 |
24,1 |
5,6 |
|
FeS2
|
Пирит
|
0,87 |
45,6 |
5,0 |
|
"
|
Марказит
|
0,84 |
44,0 |
4,9 |
|
ZnS
|
Сфалерит
|
0,65 |
34,1 |
4,1 |
|
"
|
Вюртцит
|
0,64 |
33,5 |
4,0 |
|
Cu2S
|
Халькозин гекс.
|
0,845 |
44,3 |
6,0 |
|
"
|
Халькозин ромб.
|
0,81 |
42,4 |
5,8 |
|
FeS
|
Троилит
|
1,00 |
52,4 |
4,8 |
|
Fe0.88S
|
Пирротин гекс.
|
0,95 |
49,8 |
4,65 |
|
Fe0.82S
|
Пирротин монокл.
|
0,94 |
49,3 |
4,64 |
|
α-FeOOH
|
Гетит
|
0,76 |
39,8 |
4,3 |
|
γ-FeOOH
|
Лепидокрокит
|
0,72 |
37,7 |
4,1 |
|
Mg2SiO4
|
Тип K2NiF4
|
1,1 |
57,6 |
4,1 |
|
γ-Mg2SiO4
|
Рингвудит
|
0,81 |
42,2 |
3,5 |
|
α-Mg2SiO4
|
Форстерит
|
0,77 |
40,3 |
3,2 |
Таблица 1.6
Рост параметров структурной плотности и плотности в кристаллах в зависимости от увеличения КЧ катионов
| Кристаллическая фаза с указанием КЧкатионов и структурного типа |
γ |
v, % |
ρ, г/см3 |
| Mg[6]Si[4]O3 (типа пироксена) |
0,68 |
35,6 |
3,2 |
| Mg[6]Si[6]O3 (типа ильменита) |
0,83 |
43,5 |
3,8 |
| Mg[7.5]Si[4.5]O3 (типа граната) |
0,88 |
46,1 |
3,7 |
| Mg[8]Si[6]O3 (типа перовскита) |
1,09 |
57,1 |
4,1 |
Таблица 1.7
Структурная, гравитационная и энергетическая плотности ряда модификаций SiO2 в сопоставлении с твердостью
| Модификации SiO2 |
γ |
ρ, г/см3 |
Ev, кДж/см3 |
НМ |
|
Кварц
|
0,33 |
2,65 |
83 |
7 |
|
Коэсит
|
0,37 |
2,93 |
91 |
7,5 |
|
Стишовит
|
0,72 |
4,34 |
132 |
8,5 |
|
SiO2 типа пирита
|
0,87 |
4,6 |
135 |
9,5 |
|
SiO2 типа флюорита
|
1,00 |
4,8 |
139 |
10,9 |
|
SiO2 типа котунита
|
1,15 |
5,1 |
- |
- |
Следует обратить внимание на то, что параметры γ не всегда дают корректные результаты в смысле предсказания стабильности структуры в зависимости от давления, определяемого глубиной образования. Так, по параметрам γ ряд глубинности соединений состава MgSiO
3 (таблица 1.6) таков: пироксеновый тип → ильменитовый тип → гранатовый тип → перовскитовый тип, в то время как соответствующий экспериментальный ряд с указанием давлений переходов согласно данным работы (Ohtani, Kagawa, Fujino, 1991) отличается перестановкой мест ильменитового и гранатового типов фаз состава MgSiO
3:
|
17 ГПа 22,5 ГПа 23 ГПа
|
| Пироксеновый
тип |
→ |
Гранатовый
тип |
→ |
Ильменитовый
тип |
→ |
Перовскитовый
тип |
Эти экспериментальные данные лучше интерпретируются с позиций использования параметров энергоплотности рассматриваемых кристаллических соединений состава MgSiO
3 (Зуев, 1995).
Тем не менее, представляется вполне вероятным, что параметры структурной плотности кристаллических решеток минералов могут найти применение в качестве критериев глубинности минералообразования. Некоторые соответствующие данные по этому вопросу приведены в таблице 1.8, где типичные гипогенные (глубинные) и гипергенные (поверхностные) минералы весьма четко различаются по параметру γ: средняя величина γ для первых близка к 0,9, для вторых равна 0,45.
Таким образом, средние параметры γ типичных глубинных и поверхностных минералов различаются почти в два раза, а их соответствующие средние плотности (ρ) - в 1,3 раза. Это означает, что параметр γ более чувствителен, а потому и более информативен как критерий глубинности минералообразования по сравнению с параметром ρ. Как известно, типичная глубинная порода - кимберлит имеет в своем составе оливин, флогопит, пироп, циркон, диопсид (хром-диопсид), ильменит, перовскит и апатит. Все указанные минералы характеризуются довольно высокими параметрами γ (таблица 1.8).
Таблица 1.8
Сопоставление структурной и гравитационной плотностей для ряда глубинных и поверхностных минералов
| Гипогенныеминералы |
γ |
ρ, г/см3 |
Гипергенныеминералы |
γ |
ρ, г/см3 |
|
Алмаз
|
0,65 |
3,5 |
Лед
|
0,24 |
0,92 |
|
Стишовит
|
0,72 |
4,3 |
Опал
|
0,25 |
2,2 |
|
Циркон
|
0,74 |
4,7 |
Кварц
|
0,33 |
2,65 |
|
Оливин
|
0,77 |
3,6 |
Куприт
|
0,49 |
6,1 |
|
Жадеит
|
0,80 |
3,3 |
Сера
|
0,34 |
2,1 |
|
Ильменит
|
0,82 |
4,8 |
Арсенолит
|
0,35 |
3,9 |
|
Диопсид
|
0,83 |
3,3 |
Каолинит
|
0,46 |
2,6 |
|
Флогопит
|
0,84 |
3,0 |
Гиббсит
|
0,53 |
2,4 |
|
Пироп
|
0,89 |
3,55 |
Кальцит
|
0,65 |
2,7 |
|
Апатит
|
0,93 |
3,2 |
Гидрогетит
|
<0,70 |
4,0 |
|
Троилит
|
1,00 |
4,8 |
Гипс
|
0,57 |
2,3 |
|
Периклаз
|
1,00 |
3,6 |
Аурипигмент
|
0,49 |
3,5 |
|
Перовскит
|
1,31 |
4,0 |
Реальгар
|
0,50 |
3,6 |
|
Рингвудит
|
0,81 |
3,5 |
Азурит
|
0,45 |
3,8 |
|
Средние параметры
|
<0,87> |
<3,8> |
Средние параметры
|
<0,45> |
<3,0> |
Интересно с позиций структурной плотности рассмотреть ряд глубинности минералов по И. В. Матяшу (Матяш, 1991), который связывает увеличение глубинности образования минералов с ростом их ионности (эффективных зарядов атомов кислорода) и плотности. Рост ионности, по И. В. Матяшу, приводит к образованию все более плотноупакованных, компактных структур. Значит, в этом случае вполне правомочно использование параметра структурной плотности γ соответствующих кристаллических решеток минералов.
Таблица 1.9
Ряд глубинности минералов (Матяш, 1991) в сопоставлении с параметрами: структурной плотности, ионности и удельной массовой энергии атомизации
| Минерал |
γ |
fi (Зуев, 1990) |
Em, кДж/г |
Минерал |
γ |
fi (Зуев, 1990) |
Em, кДж/г |
|
Гидроксит (вода)
|
0,25 |
0,33 |
53,9 |
Антофиллит
|
0,62 |
0,60 |
29,8 |
|
Брусит
|
0,68 |
0,57 |
34,3 |
Гиперстен
|
0,68 |
0,60 |
29,0 |
|
Кварц
|
0,33 |
0,5 |
31,3 |
Форстерит
|
0,77 |
0,64 |
27,8 |
|
Серпентин
|
0,60 |
0,54 |
31,8 |
Периклаз
|
1,00 |
0,80 |
24,7 |
|
Тальк
|
0,58 |
0,53 |
30,8 |
|
|
|
|
Как следует из таблицы 1.9, ряд глубинности минералов по И. В. Матяшу в целом подтверждается и дополнительно обосновывается использованием соответствующих параметров γ. Особое внимание заслуживает весьма тесная обратная корреляция глубинности минералов с величинами их удельной массовой энергии атомизации по Э. Мамырову (Мамыров, 1989).
Приведем также ряд других примеров прикладного использования параметров γ. По данным (Смольянинов, 1955) флюорит легко и иногда в больших количествах замещает кальцит, что можно связать с ростом γ в этом процессе:
CaCO
3 (γ = 0,65) → CaF
2 (γ = 1,0).
Аналогичным образом объясняется легкость замещения галенита англезитом:
PbS (γ = 1,0) → PbSO
4 (γ = 1,22).
Можно констатировать, что в зоне окисления многие процессы замещения одних минералов другими сопровождаются уплотнением вновь образующихся кристаллических решеток минералов, что связано с ростом параметров γ. Повышенная устойчивость малахита по сравнению с азуритом может служить тому примером:
Азурит Cu
3[CO
3]
2(OH)
2 (γ = 0,45) → малахит Cu
2[CO
3](OH)
2 (γ = 0,74).
Сульфид меди, например, халькопирит CuFeS
2 (γ = 0,65), в зоне окисления замещается ковеллином CuS (γ = 0,69), купритом Cu
2O
(γ = 0,49), самородной медью Cu (γ = 1,42), гетитом FeOOH (γ = 0,76). Как видим, параметры γ указанных продуктов замещения халькопирита заметно растут по отношению к исходной величине γ.
В качестве выводов по данному разделу можно заключить, что кристаллохимические параметры структурной плотности минералов γ определенно коррелируются с условиями (глубинностью) минералообразования, а также могут служить индикаторами (указателями) направленности процессов замещения одних минералов другими.
[1] Точнее,
n есть число самостоятельных структурных узлов кристаллической решетки, включая атомы, ионы и радикалы (комплексные ионы).

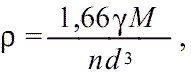 (1.3)
(1.3) 