1.2.3. Кристаллоструктурный метод расчета ионности связей и эффективных зарядов атомов в минералах
Этот метод базируется на двух основных постулатах:
Химическая связь, осуществляемая связывающими межостовными электронами, рассматривается как взаимодействие ближнего порядка (ковалентного типа), оно происходит на расстояниях, отвечающих сумме ковалентных радиусов атомов. Иными словами, предполагается, что перераспределение электронной плотности в соединении между атомами происходит в пределах их первых координационных сфер, определяемых координационными числами (
КЧ) атомов.
В химических соединениях имеет место тенденция реализации электронейтрального состояния атомов. В рамках остовно-электронного подхода это означает стремление остовов к присоединению связывающих электронов с целью реализации состояния нейтральных атомов, поскольку процесс рекомбинации электронов экзотермичен. Другое дело, что разные остовы, обладая неодинаковыми силовыми характеристиками, в различной степени способны реализовать эту тенденцию, благодаря чему и получается то или иное распределение эффективных зарядов атомов в соединениях.
Конкретная процедура оценки ионности (эффективных зарядов атомов) минералов производится в ряд этапов (Зуев, 1990):
- Находится общее число валентных электронов минерала, равное суммарному заряду остовов с обратным знаком. Проблема оценки числа участвующих в химической связи электронов у атомов в соединениях подробно рассмотрена в предыдущем разделе 1.2.2.
- Суммарное число валентных электронов минерала распределяется по соответствующим двухцентровым (межостовным) связям, т. е. оцениваются их электронные заряды.
- Электронные заряды связей делятся на доли электронного облака, локализованные у атомных остовов пропорционально их силовым характеристикам.
- Суммированием зарядов остовов и относящихся к ним долям электронных облаков вычисляются эффективные заряды атомов (ионов).
Как показано в монографии (Зуев, 1990), первый этап соответствует составлению остовно-электронной формулы (ОЭФ) соединения (минерала), второй - построению остовно-электронной модели (ОЭМ) соответствующей кристаллической структуры минерала, третий и четвертый этапы отвечают непосредственной оценке ионности связей и эффективных зарядов атомов с использованием кристаллохимических параметров соответствующей ОЭМ минерала.
В качестве примеров приведем некоторые ОЭФ минералов и молекул, в которых по сравнению с монографиями (Зуев, 1990; Зуев, Денисов, Мочалов и др., 2000) внесены (в отдельных случаях) некоторые изменения (уточнения) в отношении фактической валентности неметаллов:
| железо (α-Fe) |
- |
│[4e-(Fe8+)] (1e-)8 [(Fe8+)4e-]│КЧ = 8/2/8,
|
| алюминий |
- |
│[Al3+] (0,5e-)12 [Al3+]│КЧ = 12/2/12,
|
| алмаз |
- |
│[С4+] (2e-)4 [C4+]│КЧ = 4/2/4,
|
| куприт |
- |
│[Cu+]2 (1,5e-)4 [(O6+)2e-]│КЧ = 2/2/4,
→
|
| глет |
- |
│[2e-(Pb4+)] (1,5e-)4 [(O6+)2e-]│КЧ = 4/2/4,
→
|
| кварц |
- |
│[Si4+] (3e-)4 [(O6+)2e-]2│КЧ = 4/2/2,
→
|
| периклаз |
- |
│[Mg2+] (1e-)6 [(O6+)2e-]│КЧ = 6/2/6,
→
|
| молекула MgO |
- |
│[Mg2+] 4e- [(O6+)4e-]│КЧ=1/2/1,
→
|
| рутил |
- |
│[Ti4+] (2e-)6 [(O6+)2e-]2│КЧ = 6/2/3,
→
|
| пирит |
- |
│[Fe2+] (2e-)6 [(S6+)2e-(S6+)]│КЧ = 6/2/6,
→
|
| сфалерит |
- |
│[Zn2+] (2e-)4 [S6+]│КЧ = 4/2/4,
→
|
| галенит |
- |
│[2e-(Pb4+)] (1e-)6 [(S6+)2e-]│КЧ = 6/2/6,
→
|
| молекула PbS |
- |
│[2e-(Pb4+)] 4e- [(S6+)4e-]│КЧ=1/2/1,
→
|
| молекула СО |
- |
│[2e-(C4+)] 6e-[(O6+)2e-]│КЧ=1/2/1,
→
|
| молекула СО2 |
- |
│[4e-(O6+)] 4e- [C4+] 4e- [(O6+)4e-]│КЧ = 1/2/1/2/1,
← →
|
| кальцит |
- |
│[Ca2+] (1,21e-)6 [(O6+)2e-]3 (3,58e-)3 [C4+]│КЧ=6/2/(2+1)/2/3,
→ ←
|
| форстерит |
- |
│[Mg2+]2 (1,23e-)12 [(O6+)2e-]4 (2,31e-)4 [Si4+]│КЧ = 6/2/(3+1)/2/4,
→ ←
|
| шпинель |
- |
│[Mg2+] (1,5e-)4 [(O6+)2e-)]4 (1,5e-)12 [Al3+]2│КЧ = 4/2/(1+3)/2/6,
→ ←
|
| молекула HCl |
- |
│[H+] 2e- [(Cl7+)6e-]│КЧ = 1/2/1,
→
|
| молекула воды |
- |
│[H+]2 (2e-)2 [(O6+)4e-]│КЧ = 1/2/2,
→
|
| комплекс SO42- |
- |
│[S6+] (4e-)4 [(O6+)4e-]4│2-КЧ =4/2/1,
→
|
| барит |
- |
│[Ba2+] (0,67e-)12 [(O6+)3e-]4 (3e-)4 [S6+]│КЧ = 12/2/(3+1)/2/4,
→ ←
|
| гиббсит |
- |
│[Al3+] (2e-)6 [(O6+)2e-]3 (2e-)3 [H+]3│КЧ = 6/2/(2+1)/2/1,
→ ←
|
| флюорит |
- |
│[Ca2+] (1e-)8 [(F7+)4e-]2│КЧ = 8/2/4,
→
|
| галит |
- |
│[Na+] (1e-)6 [(Cl7+)2e-]│КЧ = 6/2/6.
→
|
В этих формулах в квадратных скобках заключены атомные остовы, между которыми в круглых скобках находятся связывающие электроны (электриды). Неподеленные электроны показаны слева от катионного и справа от анионного остовов. Стрелки означают смещение связывающих электронов (электридов) к более электроотрицательному остову неметалла, указывая на полярный характер межатомных связей, а отсутствие стрелок под электридами указывает на ковалентный характер связей. Справа за прямой скобкой остовно-электронной формулы последовательно указаны координационные числа остовов и электридов, для последних имеет место линейное окружение остовами (
КЧ = 2).
Насколько правомерно или, другими словами, отвечает реальности представление кристаллов в виде ассоциации атомных остовов и связующих (а также неподеленных) электронов-электридов, что отражают предлагаемые остовно-электронные формулы? Подробное обоснование этого подхода имеется в уже достаточно обширной литературе (Bent, 1970; Гиллеспи, 1975; Cohen, 1984; Зуев, 1990; Гиллеспи, Харгиттаи, 1992; Семенов, 2001). Поэтому ограничимся лишь некоторыми дополнительными аргументами.
Обычно ковалентную двухэлектронную связь трактуют в виде спаривания электронов у нейтральных атомов: например, Н-Н или Н
¯Н
в простейшем случае молекулы водорода Н
2. Однако эти схемы явно упрощают реальную картину ковалентной связи, природу которой раскрывают квантово-химические методы (молекулярных орбит, валентных связей), в рамках которых необходимо учитывать обмен электронами у вступающих в связь атомов. Так, по Полингу (Полинг, 1974, с.140) молекулу водорода можно записать в виде резонанса двух структур:
H
A↓H
B↑ и H
A↑ H
B↓
Это значит, что электрон с положительным спином (↓) и электрон с отрицательным спином (↑) меняются местами, т. е. происходит обмен электронами у атомов водорода.Понятно, что обмен электронами у первоначально нейтральных атомов водорода Н
А и Н
В предполагает отрыв у них электронов (с затратами энергий ионизации
Ry = 13,6 эВ), образование остовов [H
A+] и [H
B+] и локализацию в межостовном пространстве ставшей общей (связующей) пары неразличимых электронов, которые попадают под действие силовых полей обоих остовов. Описанную ситуацию как раз и отражает остовно-электронная модель молекулы водорода - |[H
+](2e
-)[H
+]|.
[1] Аналогичным образом можно обосновать и другие более сложные остовно-электронные модели молекул и кристаллов.
Имеются специальные формулы для оценки
q в кристаллах (Зуев, 1990). Так, в случае простых (бинарного состава МхХу) минералов:
q(M-X) = -(ZM/КЧМ + ZX/КЧХ), (1.25)
а в случае сложных минералов электронный заряд связи металл-неметалл находится по формуле:
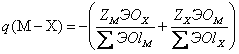 (1.26)
(1.26)
где
ZM,
ZX - числа валентных электронов атома, соответствующих зарядам остовов; Σ
ЭОlM, Σ
ЭОlX - суммы электроотрицательностей лигандов вокруг атомов М и Х в соответствующих атомных полиэдрах кристаллической структуры. Необходимые для таких расчетов координационные
ЭО атомов имеются в (Зуев, 1990).
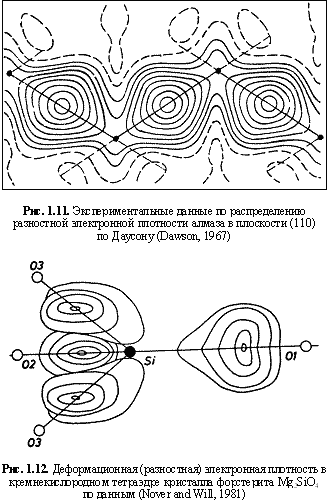
Как показано ранее в разделе 1.2.1, исходя из сферической формы остовов и связывающих электронных облаков (электридов), обладающих соответствующими размерами и зарядами (рис. 1.3), можно строить остовно-электронные модели структур минералов. На рис. 1.4-1.8 даны примеры таких моделей для рутила, алмаза, кварца, сфалерита и периклаза. Важно подчеркнуть, что эти модели фактически демонстрируют
новый остовно-электронный способ изображения кристаллических структур, в какой-то мере адекватный картам разностной электронной плотности (рис. 1.11-1.12), а также расчетам зарядовой электронной плотности в кристаллах по методу псевдопотенциала (Cohen, 1984). В последнем случае на соответствующих схемах, например, для кристалла Si, непосредственно фигурируют как связывающие электронные облака, так и остовы кремния.
Остовно-электронные модели структур можно представлять в двух используемых в кристаллохимии аспектах (Зуев, 1990):
- как постройки из сферических остовов и электридов, обладающих соответствующими зарядами и радиусами (рис. 1.4-1.8);
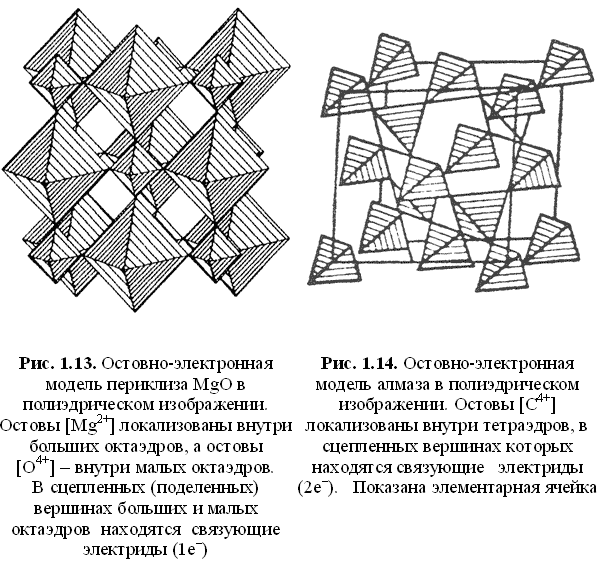
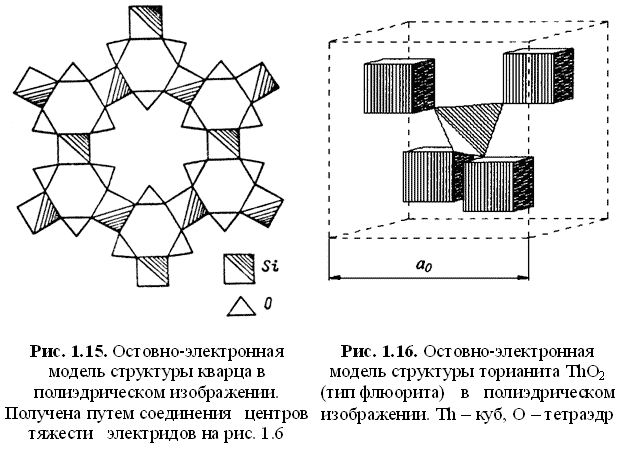
- как ассоциации остовных координационных полиэдров (рис. 1.13-1.16).
Во втором случае остовы катионных и анионных компонентов располагаются в центре соответствующих полиэдров, а связующие электроны локализованы в общих (поделенных) вершинах полиэдров. В свободных вершинах остовных полиэдров располагаются неподеленные электроны.
Полиэдрический способ изображения остовно-электронных моделей удобен и информативен: кристалл строится из сцепленных вершинами элементарных атомных (катионных и анионных) полиэдров-кирпичиков - октаэдров в структуре галита и периклаза, тетраэдров в структуре алмаза и сфалерита, кубов тория (церия) и тетраэдров кислорода в структуре торианита и церианита, октаэдров магния и тетраэдров кремния и кислорода в структуре форстерита и т. д. Согласно полиэдрическому способу изображения структуры, расстояние от центра полиэдра до общих (поделенных) вершин равно (по определению) ковалентному радиусу атома.
Найденные по формулам (1.25) и (1.26) электронные заряды связей
q(M-X) делятся между остовами пропорционально силовым параметрам
FM и
FX, в качестве которых можно использовать величины:
F = Z/(КЧxrc2) или F = Z/(Lrc2), (1.27)
где
L- общая лигандность остова, т. е. его координация с учетом неподеленных электронов.
В монографии (Зуев, 1990) приведены многочисленные расчеты
Q атомов в минералах с использованием параметров
Z и соответственно
F. Однако понятно, что одинаковые параметры
Z слабо отражают индивидуальные химические особенности таких разных катионных остовов, как [Mg2+] и [Fe2+]. Поэтому более корректно, по-видимому, в формулах (1.27) вместо номинального заряда
Z использовать суммарный эффективный заряд ядра, действующий на валентные (сверх остова) электроны атома - Σ
Zi*. Тогда эти формулы пре-образуются в:
F* = (ΣZi*)/(КЧxrc2) или F* = (ΣZi*)/(Lrc2), (1.28)
где
Zi* - действующий на валентный электрон эффективный заряд ядра, вычисляемый по правилам С. С. Бацанова (Бацанов и Звягина, 1966; Бацанов, 1986), либо рассчитываемый из потенциалов ионизации атома по формуле (1.12). Именно второй способ оценки эффективных зарядов ядер, как более простой, принят в данной работе.
Использованием эффективных зарядов ядер в формулах (1.28) удается в явной форме, хотя и в суммарно усредненном виде, учесть силовые характеристики атома для всех его сверхостовных электронов. Так, в случае муассанита SiC, остовно-электронная формула которого |[Si
4+] (2e
-)
4 [C
4+]|, совершенно очевидна необходимость учета эффективных зарядов ядер для всех четырех валентных электронов атомов Si и C при оценке их силовых параметров.
Вычисленные по формулам (1.27) или (1.28) силовые параметры используются для расчета ионного (полярного) характера связей М-Х кристалла:
λ(М-Х) = (FX - FM)/(FX + FM) (1.29)
λ(М-Х) = (FX* - FM*)/(FX* + FM*) (1.30)
Многочисленные расчеты показали близость оценок ионности связей в минералах по обеим формулам, хотя вторая из них предпочтительнее.
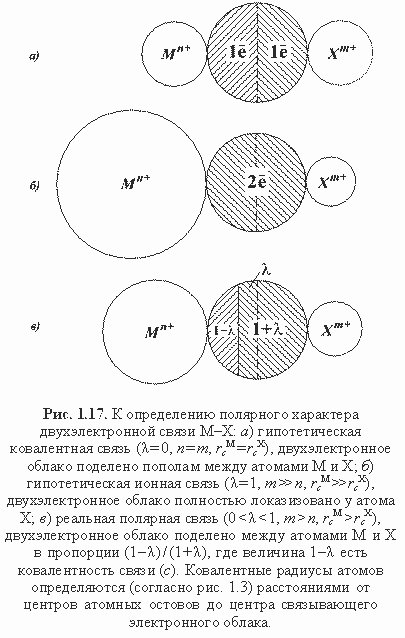
Схема полярной связи М-Х приведена на рис. 1.17, где чисто ионная связь (λ = 1) является лишь условной абстракцией. На самом деле прообразом такой связи является, например, неподеленная пара электронов при остове кислорода в кварце (рис. 1.6). В этом случае ввиду отсутствия второго (катионного) остова можно принять
FM =
FM* = 0, тогда по формулам (1.29) и (1.30) λ = 1, т. е. неподеленную пару при остове можно отождествить с химической двухэлектронной связью 100%-полярности. Поскольку в реальных связях М-Х с двумя остовами всегда
FM > 0 и
FM* > 0, то чисто ионные связи в гетероатомных химических соединениях (минералах) невозможны, соответственно нереальны предельно-ионные структуры типа Na
+Cl
-, Mg
2+O
2-, Al
23+O
32- и др. Впрочем, это не означает, что по распределению зарядов реальные кристаллические соединения не могут быть весьма близки к предельно-ионным моделям типа указанных, о чем свидетельствуют современные данные расчетов электронной плотности.
Заключительная процедура вычисления эффективных зарядов атомов в минералах производится по следующим формулам (Зуев, 1990):
QM = ZM - КЧМN(1 - λ), QX = ZX - КЧХN(1 + λ), (1.31)
где
N - порядок связи М-Х, равный
q/2.
Возможен расчет
Q атомов в минералах на основе величин параметров
q, минуя параметры λ. Обозначим через
с - электронную долю связи, локализованную на катионном компоненте, а через
q-
c соответственно - на анионном компоненте связи М-Х. Тогда из пропорции
с/(q-
c) =
FM*/
FX*имеем:
с = (qFM*)/(FM*+FX*), q-c = (qFX*)/(FM*+FX*). (1.32)
Зная
КЧ атомов М и Х в структуре минерала, приходим к следующим формулам:
QM = ZM - КЧМс, QX = ZX - КЧХ(q-c), (1.33)
которые дают те же самые результаты, что и формулы (1.31).
Для сопоставления вычисленных по разработанной методике Q атомов в кристаллических соединениях с соответствующими данными их диэлектрической ионности по Филлипсу-Ван Фехтену рекомендуется выражение:
fi = Q/Qи, (1.34)
представляющее собой степень ионизации атомов, равную отношению эффективных зарядов к предельно-ионным зарядам атомов. В монографии (Зуев, 1990) даны примеры хорошего соответствия оценок эффективных зарядов атомов в кристаллах в рамках двух указанных подходов.
Разработанная методика оценки ионности (эффективных зарядов атомов) универсальна в том смысле, что применима к соединениям различного типа, будь то молекулы, кристаллы, комплексы и т. д. Соответственно она была успешно апробирована на большом числе минералов и искусственных соединений. Для расчетов были использованы эффективные заряды ядер для валентных электронов атомов согласно (Zhang, 1982), электронные заряды связей в соединениях рассчитывались по приведенным формулам, либо непосредственно заимствовались из книги (Зуев, 1990). Ковалентные радиусы неметаллических компонентов
rc(X) были приняты с учетом данных Слэтера, Урусова, Лебедева (Лебедев, 1969; Урусов, 1975; Зуев, 1990), а металлических - находились по разности
rc(M) =
d(M-X) -
rc(X), где
d(M-X) - среднее межатомное расстояние катион-анион в структуре.
В качестве примеров рассчитаем эффективные заряды атомов в молекуле NaCl, галите NaCl, cфалерите ZnS, периклазе MgO, кварце SiO
2, форстерите Mg
2SiO
4 и бишофите MgCl
2(H
2O)
6.
Остовно-электронная формула молекулы NaCl - |[Na
+]2e
-[(Cl
7+)6e
-]|, она обладает ординарной полярной связью Na-Cl. Размерные характеристики молекулы:
d(Na-Cl) = 2,36 Å,
rc(Cl) = 0,7 Å,
rc(Na) = 1,66 Å. Эффективные заряды ядер для остовов Σ
Zi*(Na
+) = 1,78, Σ
Zi*(Cl
+) = 2,82, по формулам (1.28)
F*(Na
+) = 1,78/1,662 = 0,646,
F*(Cl+) = 2,82/0,72 = 5,755, по формуле (1.30) l(Na-Cl) = (5,755 - 0,646)/(5,755 + 0,646) = 0,8, т. е. получаем Na+0.8Cl-0.8, что соответствует ионности, вычисленной из дипольного момента молекулы NaCl (Бацанов, 1986).
Остовно-электронная формула галита была приведена выше,
q(Na-Cl) = 1e-,
d(Na-Cl) = 2,82 Å,
rc(Cl) = 1,0 Å,
rc(Na) = 1,82 Å, в этом случае
F*(Na
+) = 1,78/(6x1,822) = 0,09,
F*(Cl
5+) = 23,76/(6x12) = 3,96. По формуле (1.30) λ(Na-Cl) = 0,96 и далее по формулам (1.31):
Q(Na) = 1 - 6x0,5(1 - 0,96) = +0,88,
Q(Cl) = 5 - 6x0,5(1 + 0,96) = -0,88, т. е. для галита имеем Na
+0.88Cl
-0.88, что соответствует диэлектрической ионности кристалла NaCl (Бацанов, 1982). Обратим внимание на заметный рост эффективных зарядов атомов при переходе от молекулы к кристаллу.
В сфалерите ZnS
КЧ атомов равны 4,
q(Zn-S) = 2e
-,
d(Zn-S) = 2,35 Å,
F*(Zn
2+) = 6,83/(4x1,35
2) = 0,94,
F*(S
6+) = 30,35/(4x1
2) = 7,59, по формуле (1.30) λ(Zn-S) = 0,78 и далее по формулам (1.31), в которых
N = 1:
Q(Zn) = 2 - 4(1 - 0,78) = +1,12 и
Q(S) = 6 - 4(1 + 0,78) = -1,12, т. е. для сфалерита получаем Zn
+1.12S
-1.12.
В периклазе MgO (рис. 1.8)
КЧ обоих атомов равны 6,
q(Mg-O) = 1e
-,
d(Mg-O) = 2,10 Å,
rc(O) = 0,55 Å,
rc(Mg) = 1,55 Å, S
Zi*(Mg
2+) =
= 5,21, S
Zi*(O
4+) = 13,94,
F*(Mg
2+) = 5,21/(6x1,55
2) = 0,361,
F*(O
4+) = 13,94/(6x0,55
2) = 7,68. По формуле (1.30) находим λ(Мg-O) = 0,91 и далее по формулам (1.31)
Q(Mg) = 2 - 6x0,5(1 - 0,91) = +1,73,
Q(O) = 4 - 6x0,5(1 + 0,91) = -1,73. В итоге получаем для периклаза Mg
+1.73O
-1.73.
В случае кварца SiO
2 (рис. 1.6)
КЧ(Si) = 4(O),
КЧ(О) = 2(Si),
q(Si-O) = 3e-,
d(Si-O) = 1,61 Å,
rc(O) = 0,55 Å,
rc(Si) = 1,06 Å, S
Zi*(Si
4+) = 15,205, S
Zi*(O
4+) = 13,94,
F*(Si4+) = 15,205/(4x1,06
2) = 3,383,
F*(O4+) = 13,94/(2x0,55
2) = 23,04. По формуле (1.30) λ(Si-O) = 0,744 и далее по формулам (1.31) находим:
Q(Si) = 4 - 4x1,5(1 - - 0,744) = +2,46,
Q(O) = 4 - 2x1,5(1 + 0,744) = -1,23. Таким образом, для кварца имеем Si
+2.46O
2-1.23, что соответствует его диэлектрической ионности
fi = 0,6 (Бацанов, 1982).
В форстерите Mg
2SiO
4, структура которого характеризуется
КЧ(Mg) = 6(O),
КЧ(Si) = 4(O) и
КЧ(О) = 3Mg+Si, усредненные электронные заряды связей, межатомные расстояния и ковалентные радиусы атомов:
q(Mg-O) = 1,23e
-,
q(Si-O) = 2,31e
-,
d(Mg-O) = 2,12 Å,
d(Si-O) = 1,63 Å,
rc(Mg) = 1,57 Å,
rc(Si) = 1,08 Å,
rc(O) = 0,55 Å. Суммарные эффективные заряды ядер для валентных электронов атомов - Σ
Zi*(Mg
2+) = 5,21, Σ
Zi*(Si
4+) = 15,205, Σ
Zi*(O
4+) = 13,94, силовые параметры остовов -
F*(Mg
2+) = 5,21/(6x1,57
2) = 0,352,
F*(Si
4+) = 15,205/(4x1,08
2) = 3,259,
F*(O
4+) = 13,94/(4x0,55
2) = 11,521. По формуле (1.30) λ(Mg-O) = 0,941, λ(Si-O) = 0,559 и далее по формулам (1.31):
Q(Mg) = 2 - 6x0,615(1 - 0,941) = +1,782,
Q(Si) = 4 - 4x1,155(1 - 0,559) = +1,963,
Q(O) = 4 - 3x0,615(1 + 0,941)-1x1,155(1 + 0,559) = -1,382, т. е. приходим к Mg
2+1.78Si
+1.96O
4-1.38. Найденные в форстерите эффективные заряды оказались удивительно близкими к полученным японскими учеными из прецизионных расчетов электронной плотности - Mg
2+1.75Si
+2.1O
4<-1.4> (Fujino, Sasaki, Takeuchi, Sadanada, 1981).
В качестве заключительных примеров расчета
Q атомов рассмотрим комплексные кристаллические соединения.
Бишофит, как показали структурные исследования, имеет молекулярную структуру, состоящую из октаэдрических комплексов [Mg(H
2O)
6]
2+, нейтрализованных двумя ионами Cl
-. Соответственно формула минерала - [Mg(H
2O)
6]
2+Cl
2-, а структурная формула отдельного иона [Mg(H
2O)
6]
2+:
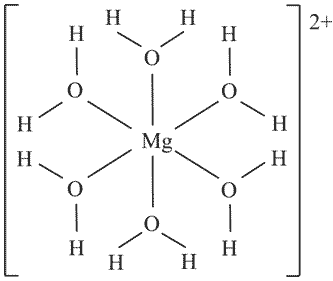
Здесь атом кислорода, имея плоско-треугольную координацию -
КЧ(О) = Mg+2H, находится, по-видимому, в состоянии 3s2p
2-гибридизации с неподеленной парой 2s
2-электронов, и соответственно с остовом [O
4+]. Межатомные расстояния:
d(Mg-O) = 2,08 Å,
d(H-O) = 1,0 Å, ковалентные радиусы:
rc(Mg) = 1,53 Å,
rc(H) = 0,43 Å,
rc(O) = 0,55 Å. Исходное распределение заряда в комплексе - [Mg2+(H
2O)
6], т. е. число валентных электронов у атома магния равно нулю. Тогда расчет по формуле (1.26) дает
q(Mg-O) = -[(0x3,5)/(6x3,5) + (4x1,3)/(1,3 + 2x2,1)] = 0,945e
-,
q(H-O) = -[(1x3,5)/(1x3,5) + (4x2,1)/(1,3 + 2x2,1)] = 2,527e
-. Силовые параметры остовов:
F*(Mg
2+) = 5,21/(6x1,53
2) = 0,37,
F*(H
+) = 0,85/(1x0,43
2) = 4,6,
F*(O
4+) = 13,94/(3x0,55
2) = 15,36. Воспользовавшись в данном случае формулами (1.32), для связи Mg-O находим
с = 0,0224e
-,
q-
c = 0,9231e
-, а для связи H-O
c = 0,5824e
-,
q-
c = 1,9446e
-. Далее по формулам (1.33) находим
Q(Mg) = 2 - 6x0,0224 = +1,866,
Q(H) = 1 - 1x0,5824 = +0,417,
Q(O) = 4 - 1x0,9231 - 2x1,9446 = -0,812. Результирующее распределение зарядов атомов в бишофите оказалось следующим - [Mg
+1.866x(H
2+0.417O
-0.812)
6]
2+Cl
2-. Баланс зарядов в молекуле воды приводит к (H
2O)
+0.022, что позволяет понять природу примеси ковалентной составляющей связи в данном и других аква-комплексах.
[2] Как это очевидно, дело заключается в незначительной перекачке электронной плотности от молекул воды на свободные орбитали центрального катиона. Результатом этого является некоторое уменьшение формального заряда центрального катиона и соответственно - появление на молекулах воды указанного избыточного положительного заряда. Другими словами, от каждой из шести первоначально электронейтральных молекул воды на свободные орбитали центрального катиона (Mg
2+) переходит 0,022e-, и он приобретает эффективный заряд +2 - 0,022x6 = +1,868.
В случае бианкита ZnSO
4x6H
2O конституцию этого минерала можно рассматривать как соединение из октаэдрических и тетраэдрических комплексных ионов - [Zn(H
2O)
6]
2+ и [SO
4]
2-. Расчет приводит к следующим эффективным зарядам атомов в октаэдрическом комплексе [Zn
+1.83(H
2+0.418O
-0.807)
6]
2+. Эффективные заряды атомов в комплексе [SO
4]
2- вычислены для структуры с двойными связями и следующими параметрами:
d(S-O) = 1,50 Å,
rc(O) = 0,5 Å,
rc(S) = 1,0 Å,
q(S-O) = 4,0e
-,
F*(S
6+) = 30,35/(4x1
2) = 7,59,
F*(O
2+) = 5,19/(1x0,52) = 20,76. Использование этих параметров приводит к следующим эффективным зарядам в сульфатном комплексе– [S
+1.72O
4-0.93]
2-, а общее распределение зарядов в бианките будет таковым: [Zn
+1.83(H
2+0.418xO
-0.807)
6]
2+[S
+1.72O
4-0.93]
2-. Для водного сульфата FeSO
4×6H
2O аналогичные расчеты приводят к следующему распределению эффективных зарядов - [Fe
+1.86(H
2+0.411O
-0.80)
6]
2+[S
+1.72O
4-0.93]
2-.
Для октаэдрического аква-комплекса Fe(III) расчеты дали такие эффективные заряды атомов - [Fe
+2.69(H
2+0.424O
-0.796)
6]
3+.
Для безводных сульфатов M(II)SO
4, структура которых характеризуется следующей взаимной координацией атомов:
КЧ(М) = 2О
А + 4О
В,
КЧ(S) = 2O
A + 2O
B,
КЧ(О
А) = M + S,
КЧ(О
В) = 2М + S, получились в порядке уменьшения
Q(M) такие данные:
Mn+1.843[S+1.418O2(A)-0.662O2(B)-1.969]
Mg+1.837[S+1.577O2(A)-0.70O2(B)-1.01]
Fe+1.812[ S+1.50O2(A)-0.677O2(B)-0.979]
Cu+1.812[S+1.577O2(A)-0.696O2(B)-0.998]
Co+1.806[ S+1.577O2(A)-0.695 O2(B)-0.996]
Zn+1.793[S+1.577O2(A)-0.693O2(B)-0.991]
Ni+1.788[S+1.577O2(A)-0.692O2(B)-0.99]
Обратим внимание на антибатный ход изменения эффективных зарядов нерадикальных катионов M(II) и радикальных катионов S(VI) в рассмотренном ряду сульфатов и некоторое уменьшение Q(S) при переходе от свободного радикала [SO
4]
-2 к связанному в кристаллической решетке безводному сульфату.
В таблице 1.32 приведены результаты оценок эффективных зарядов в ряде комплексов и молекул с плоско-треугольной и тетраэдрической координацией центрального атома кислородными лигандами.
Таблица 1.32
Эффективные заряды атомов в некоторых комплексах и молекулах, рассчитанные в предположении двойных связей «катион-кислород»
| Комплекс (молекула) |
d(M-On),Å |
Эффективныезаряды атомов |
Комплекс |
d(M-O4),Å |
Эффективные заряды атомов |
| [NO3]- |
1,24 |
N+0,58O3-0.527 |
[ClO4]- |
1,51 |
Cl+1.81O4-0.703 |
| [CO3 ]2- |
1,28 |
C+1O3-1 |
[MnO4]- |
1,59 |
Mn+2.22O4-0.805 |
| [SO4 ]2- |
1,50 |
S+1.72O4-0.93 |
[CrO4 ]2- |
1,65 |
Cr+2.53O4-1.133 |
| ArO4 |
1,50 |
Ar+1.94O4-0.485 |
[WO4 ]2- |
1,80 |
W+2.8O4-1.2 |
| FeO4 |
1,50 |
Fe+2O4-0.5 |
[MoO4 ]2- |
1,83 |
Mo+3.06O4-1.26 |
В рамках продемонстрированного подхода были выполнены расчеты
Qатомов в тех же минералах, что и в монографии (Зуев, 1990, стр. 55, таблица 3.9), в результате выяснилась близость расчетных эффективных зарядов атомов в обоих случаях и подтвердились три общих закономерности распределения этих зарядов в сложных минералах: 1) явление (или эффект) взаимного влияния катионов (ВВК); 2) различие в эффективных зарядах кристаллохимически нетождественных (по числу или сорту координирующих катионов) анионов, например, кислорода, обозначаемых О
А, О
В, О
Си т. д.; 3) выполнения известного второго правила Л. Полинга о локальной компенсации ионных зарядов в структуре, если в качестве таковых использовать рассчитанные величины
Q атомов.
Эффект ВВК проиллюстрируем следующими уравнениями с указанием эффективных зарядов атомов:
Mg+1.73O-1.73+Si+2.46O2-1.23 = Mg+1.79Si+2.20O3<-1.33>;
2Mg+1.73O-1.73+Si+2.46O2-1.23 = Mg2+1.78Si+1.96O4-1.38;
Al2+2.38O3-1.587+Si+2.46O2-1.23 = Al2+2.44Si+2.14O5<-1.404>;
Zr+3.21O2<-1.61>+Si+2.46O2-1.23 = Zr+3.36Si+2.14O4-1.375,
т. е. в сложном минерале (энстатите, форстерите, кианите, цирконе) по сравнению с простыми составляющими оксидами (периклазом, кварцем, корундом, бадделеитом,) происходит увеличение
Q (уменьшение ковалентности связи) более слабого катиона (Mg, Al, Zr) за счет уменьшения
Q (роста ковалентности связи) более сильного катиона (Si).
Подробно эффекты ВВК в сложных минералах рассмотрены в монографии (Зуев, 1990), однако по поводу эффектов ВВК необходимо сделать весьма существенное дополнение, упущенное в указанной монографии. В самом деле, как меняется ионность (ковалентность) связей при переходе от исходных простых составляющих к сложному минералу? Для выяснения данного вопроса сравним средние параметры ионности
fi и ковалентности (
fc = 1-
fi) для простых составляющих кристаллов, с одной стороны, и для соответствующего сложного соединения, с другой стороны. Такие сравнительные оценки удобно произвести по анионным компонентам соединений с использованием формулы 1.34, примеры соответствующих оценок приведены в таблице 1.33.
По данным последнего (пятого) столбца таблицы 1.33 четко выявляется не имеющая исключений закономерность понижения ионности и роста ковалентности в сложном кристалле относительно этого параметра (естественно, среднего) в соответствующих простых составляющих кристаллах.
Расчеты показали, что аналогичная картина имеет место и в случае содержащих более двух сортов катионов сложных кристаллических соединений, например: Ca
3Al
2Si
3O
12 (Δ
fi/D
fc = -0,07/+0,07), Mg
3Al
2Si
3O
12 (Δ
fi/D
fc = -0,04/+0,04), CaTiSiO
5 (Δ
fi/Δ
fc = -0,05/+0,05), Be
3Al
2Si
6O
18 (Δ
fi/Δ
fc = -0,02/+0,02) и т. д.
Таблица 1.33
Характер изменения параметров ионности и
ковалентности в сложных кристаллических соединениях
по сравнению с простыми составляющими кристаллами
| Q атомов в простых кристаллах |
fi/fc |
Q атомов в сложном кристалле |
fi/fc |
Dfi/Dfc |
|
Mg+1.73O-1.73, Si+2.46O2-1.23
|
0,70/0,30 |
Mg+1.79Si+2.2O3-1.33
|
0,67/0,33 |
-0,03/+0,03 |
|
2Mg+1.73O-1.73, Si+2.46O2-1.23
|
0,74/0,26 |
Mg2+1.78Si+1.96O4-1.38
|
0,69/0,31 |
-0,05/+0,05 |
|
Al2+2.38O3-1.587, Si+2.46O2-1.23
|
0,72/0,28 |
Al2+2.44Si+2.14O5-1.404
|
0,70/0,30 |
-0,02/+0,02 |
|
Fe+1.692O-1.692, W+3.94O3-1.313
|
0,70/0,30 |
Fe+1.74W+3.57O4-1.33
|
0,66/0,34 |
-0,04/+0,04 |
|
Ca+1.80O-1.80, W+3.94O3-1.313
|
0,72/0,28 |
Ca+1.87W+2.41O4-1.07
|
0,54/0,46 |
-0,18/+0,18 |
|
Ca+1.80O-1.80, Ti+3.08O2-1.54
|
0,81/0,19 |
Ca+1.89Ti+2.605O3-1.5
|
0,75/0,25 |
-0,06/+0,06 |
|
Fe+1.692O-1.692, Ti+3.08O2-1.54
|
0,80/0,20 |
Fe+1.745Ti+2.945O3-1.563
|
0,78/0,22 |
-0,02/+0,02 |
|
Zr+3.21O2-1.61, Si+2.46O2-1.23
|
0,71/0,29 |
Zr+3.36Si+2.14O4-1.375
|
0,69/0,31 |
-0,02/+0,02 |
|
2Be+1.60O-1.60, Si+2.46O2-1.23
|
0,71/0,29 |
Be2+1.65Si+2.21O4-1.38
|
0,69/0,31 |
-0,02/+0,02 |
|
2Fe+1.692O-1.692, Si+2.46O2-1.23
|
0,73/0,27 |
Fe2+1.754Si+1.90O4-1.352
|
0,68/0,32 |
-0,05/+0,05 |
|
Fe+1.692O-1.692, Nb2+3.756O5-1.502
|
0,77/0,23 |
Fe+1.748Nb2+3.628O6-1.5
|
0,75/0,25 |
-0,02/+0,02 |
ПРИМЕЧАНИЕ. Для сложных кристаллов параметр ионности fi вычисляется с использованием эффективного заряда аниона (кислорода) непосредственно по формуле 1.34. При нахождении среднего параметра fi для простых составляющих кристаллов сначала находим усредненный эффективный заряд аниона, например, для пары СaO+TiO2 Q(O) = (-1,80 + (-1,54)x2)/3 = -1,627 и далее по формуле (1.34) fi = (-1,627)/(-2) = 0,813.
В соединениях с разносортными катионами и анионами, например, в топазе, установленная закономерность сохраняется:
2/3Al2+2.38O3-1.587 + 2/3Al+2.592F3-0.864 + Si+2.46O2-1.23 = Al2+2.50Si+2.193O4-1.44F2-0.72 (Δfi/Δfc = -0,04/+0,04).
В свете установленной закономерности полученные в рамках компьютерного моделирования структур эффективные заряды (Урусов, Оганов, Еремин, 1998) в кристаллах: Al
2+1.86O
3-1.24 + Si
+1.92O
2-0.96 = Al
2+1.83Si
+2.08O
5-1.15 с противоположным (по сравнению со всеми предыдущими соответствующими данными таблицы 1.33) изменением величин в параметрах Δ
fi/Δ
fc = +0,01/-0,01 не могут считаться корректными, поскольку находятся в противоречии с эффектом ВВК. Сказанное подтверждают данные изучения этих кристаллов методом ЭСХА (РФЭС) (таблица 1.34).
Таблица 1.34
Энергии связи остовных электронов атомов в кристаллах по данным
(Диков, Брытов и др., 1979; Нефедов, 1984)
| Кристаллы (минералы) |
Al 2p, eV |
Si 2p, eV |
O 1s, eV |
| Al2O3 (корунд) |
74,2 |
- |
530,9 |
| SiO2 (кварц) |
- |
103,5 |
532,9 |
| Al2SiO5 (кианит) |
74,7 |
102,6 |
532,1 |
Поскольку в методе ЭСХА энергии связи остовных электронов катионных компонентов и их эффективные заряды находятся в прямой (симбатной) зависимости, то эти данные подтверждают найденное нами взаимосогласованное распределение эффективных зарядов атомов Al и Si в корунде, кварце и кианите (таблица 1.34). Что же касается полученного соотношения эффективных зарядов атомов Al и Si в указанной тройке минералов согласно расчетам (Урусов, Оганов, Еремин, 1998), то приходится констатировать их несоответствие экспериментальным данным метода ЭСХА.
Вопрос о том, как меняется ионность и ковалентность при переходе от простых составляющих к сложному кристаллическому соединению, является принципиальным и очень важным, объясняя причину распространенности среди минералов сложных кристаллических соединений. Так, установленный при этом рост ковалентности (снижение ионности) ведет, по нашему мнению, к энергетической стабилизации сложного соединения, термодинамическим выражением которой может, очевидно, служить превышение его энтальпии над суммой энтальпий простых составляющих соединений (Зуев, 1990). Другими словами, отрицательную величину энтальпии образования сложного кристаллического соединения (например, оксида) из простых составляющих оксидов вполне логично и обоснованно можно связать с соответствующим ростом ковалентности первого по сравнению со средней ковалентностью вторых. В частности, получают объяснение: почти двукратное увеличение энтальпии образования из оксидов форстерита Mg
2SiO
4 (Δ
fc = +0,05, Δ
Hoox = -58 кДж/моль) по сравнению с энстатитом MgSiO
3 (Δ
fc = +0,03, Δ
Hoox = -36 кДж/моль), низкая величина энтальпии образования из оксидов кианита Al
2SiO
5 (Δ
fc = +0,02, Δ
Hoox = -8 кДж/моль) и, наоборот, весьма высокая величина энтальпии образования из оксидов шеелита CaWO
4 (Δ
fc = +0,18, Δ
Hoox = -162 кДж/моль) и т. д. Попытка построения соответствующей корреляции (рис. 1.18) привела к следующей эмпирической формуле:
-ΔHoox(кДж/моль) = 40,425Ln(Δfc) + 212. (1.35)
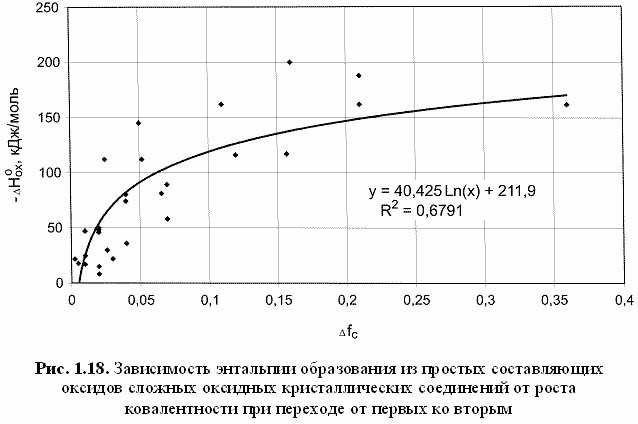
Следует признать, что эта формула дает очень грубые оценки энтальпии образования сложного оксида из простых составляющих оксидов, гораздо более корректные результаты дают изложенные в других наших работах (Zuev, 1987; Зуев, 1990) соответствующие методики.
В заключение раздела на примере форстерита Mg
2SiO
4 покажем, как влияет принятие различных параметров
Z,
Z* и
rc на результаты расчетов эффективных зарядов атомов в рамках кристаллоструктурного метода. С этой целью ниже приводятся следующие две серии данных:
|
Параметры: Z(Mg) = +2
Z(Si) = +4
Z(O) = +4
|
Параметры: ΣZi*(Mg2+) = +5,206
ΣZi*(Si4+) = +15,205
ΣZi*(O4+) = +13,94
|
|
Mg2+1.64Si+1.66O4-1.235
Mg2+1.71Si+2.10O4-1.355
Mg2+1.77Si+2.487O4-1.507
|
Mg2+1.72Si+1.50O4-1.235
Mg2+1.78Si+1.96O4-1.38
Mg2+1.83Si+2.37O4-1.507
|
В обоих случаях первый вариант эффективных зарядов (верхние строки) отвечают расчетам при
rc(O) = 0,6 Å, второй вариант (средние строки) -
rc(O) = 0,55 Å, третий вариант (нижние строки) -
rc(O) = 0,5 Å. Соответствующие ковалентные радиусы катионных компонентов (Mg, Si) находились по разности экспериментальных межатомных расстояний и фиксированных величин
rc(O).
Из приведенных данных следует вывод о заметном влиянии на результаты расчетов эффективных зарядов атомов лишь параметров ковалентных радиусов, что было установлено ранее (Зуев, Денисов, Мочалов и др., 2000). Оптимальные заряды получаются, как нам представляется, по второму варианту расчета.
В качестве заключительного по материалам первой главы выводов можно отметить следущее.
Представленный в этой главе остовно-электронный подход дает основы современных представлений о конституции и химической связи в кристаллах, что является ключом к пониманию в них энергетики межатомного взаимодействия и объяснению (предсказанию) их разнообразных физико-химических свойств.
[1] В использованном Полингом способе изображения - H
A(↓↑)H
B или H
A(↑↓)H
B.
[2] Расчет эффективных зарядов в приближении остовно-электронного подхода для свободной молекулы воды дает H
2+0.34O
-0.68 в хорошем согласии с расчетами из дипольного момента и электроотрицательностей.

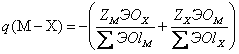 (1.26)
(1.26)




